Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chắc chắn đúng nha!
a)46=2*23
69=3*23
2116=2^2*23^2
ƯCLN(46;69;2116)=23
Ư(23)={1;23}
b)195=3*5*13
1890=2*3^3*5*7
2015=5*13*31
BCNN(195;1890;2015)=3^3*5*13*2*31=761670
761670 chiaa hết cho 5
Vì các số có chữ số tận cùng là 0;5 đều chia hết cho 5

4n+3 chia hết cho 2n-1
=> 4n-2+5 chia hết cho 2n-1
=> 2.(2n-1)+5 chia hết cho 2n-1
mà 2.(2n-1) chia hết cho 2n-1
=> 5 chia hết cho 2n-1
=> 2n-1 \(\in\)Ư(5)={1; 5}
+) 2n-1=1
=> 2n=2
=> n=1
+) 2n-1=5
=> 2n=6
=> n=3
Vậy n \(\in\){1; 3}.

﴿ gọi 3 số tự nhiên liên tiếp là a ; a+1 ; a+2 ﴾ a thuộc N ﴿
ta có : a+﴾a+1﴿+﴾a+2﴿=3a+3=3 . ﴾ a + 1 ﴿ chia hết cho 3
vậy tổng của 3 số liên tiếp chia hết cho 3
uk hồi mình thi cũng có câu này
Ta có: 3 số tự nhiên liên tiếp có dạng: a, a+1; a+2
Tổng của chúng là: a+(a+1)+(a+2)=3a+3=3(a+1) chia hết cho 3 => Đpcm

B1
Xếp hàng 3,4,8 đủ hàng
=>số hs là BCNN(3,4,8)
BCNN(3,4,8)=48
vậy số hs =....
Bài 1 ; 48
Bài 2;
a)0,1,4
b)Không chia hết cho 2,chia hết cho 5 , vì tổng trên có kq là 18,145

~~chúc bạn làm bài tốt~~
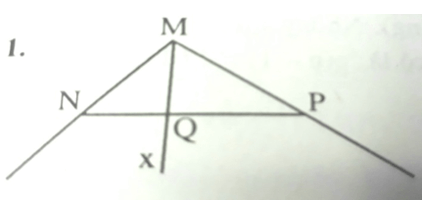
Đề kiểm tra 1:Bài 1. (2 điểm) Lấy 3 điểm không thẳng hàng M , N, P. Vẽ hai tia MN, MP sau đó vẽ tia Mx cắt đoạn thẳng NP tại Q nằm giữa N, P.
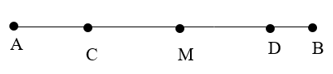
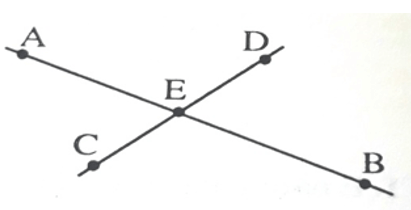
Bài 2. (3 điểm) Điểm M nằm giữa hai điểm A và B; điểm C nằm giữa hai điểm A và M, điểm D nằm giữa hai điểm M và B.
a) Tia MC trùng với tia nào? Vì sao ?
b) Tia MD trùng với tia nào? Vì sao ?
c) Điểm M có nằm giữa hai điểm C và D không? Vì sao?
Bài 3. (1 điểm) Cho trước một số điểm. Cứ qua hai điểm vẽ một đoạn thẳng. Biết rằng có 55 đoạn thẳng. Hỏi có bao nhiêu điểm cho trước?
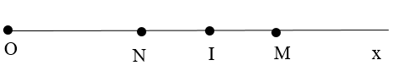
Bài 4. (4 điểm) Trên tia Ox lấy hai điểm M, N sao cho OM = 8 cm, ON = 4 cm. Gọi I là trung điểm MN.
a) Chứng tỏ rằng N là trung điểm của đoạn thẳng OM.
b) Tính IM
Đáp án và Hướng dẫn giải
Bài 1.
Bài 2.
a) Vì C nằm giữa A, M nên hai tia MA , MC trùng nhau.
b) Vì D nằm giữa M, B nên hai tia MD , MB trùng nhau.
c) Vì M nằm giữa A, B nên hai tia MA , MB đối nhau. Mà hai tia MC, MA trùng nhau, hai tia MD, MB trùng nhau. Do vậy hai tia MC, MD đối nhau
Suy ra điểm M nằm giữa C và D.
Bài 3.
Gọi số điểm cho trước là n (n ∈ N*)
Vẽ từ 1 điểm bất kì với n – 1 điểm còn lại, ta được n – 1 đoạn thẳng.
Với n điểm, nên có n(n – 1) (đoạn thẳng). Nhưng mỗi đoạn thẳng đã được tính 2 lần. Do đó số đoạn thẳng thực sự có là: n(n – 1) : 2 (đoạn thẳng)
Theo đề bài ta có:
n(n – 1) : 2 = 55
n(n – 1) = 55 . 2
n(n – 1) = 110
n(n – 1) = 11 . 10
n = 11
Vậy có 11 điểm cho trước
Bài 4.
a) Trên tia Ox có M, N và ON < OM (vì 4 cm < 8 cm ), nên N nằm giữa O và M
Do đó ON + MN = OM
4 + MN = 8
MN = 8 – 4 = 4 (cm)
Vì N nằm giữa O và M và ON = MN ( =4cm ) nên N là trung điểm của đoạn thẳng OM.
b) I là trung điểm của đoạn thẳng MN nên
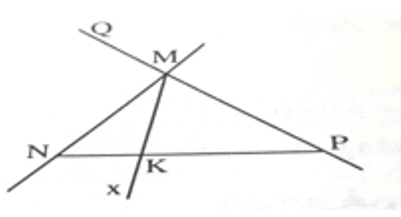
Bài 1. (2 điểm) Vẽ hình theo trình tự sau:
Cho ba điểm M, N,P không thẳng hàng
- Vẽ tia MP, đoạn thẳng NP và đường thẳng MN
- Vẽ tia MQ là tia đối của tia MP
- Vẽ tia Mx cắt đoạn thẳng NP tại K
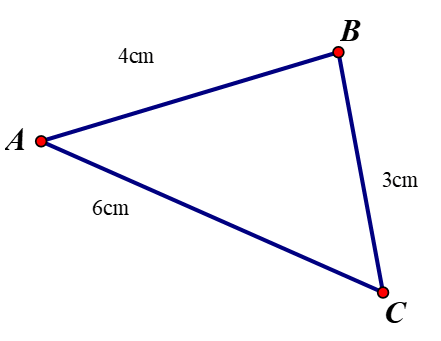
Bài 2. (3 điểm) Cho 3 điểm A, B, C biết: AB = 4cm, BC = 3 cm, AC = 6 cm. Chứng tỏ rằng:
a) Trong 3 điểm A, B, C không có điểm nào nằm giữa hai điểm còn lại
b) Ba điểm A, B, C không thẳng hàng
Bài 3. (5 điểm)
Trên tia Ax lấy các điểm B, C sao cho AB = 4 cm, AC = 8cm
a) Trong ba điểm A, B, C điểm nào nằm giữa hai điểm còn lại? Vì sao?
b) Chứng tỏ B là trung điểm của đoạn thẳng AC
c) Gọi D là trung điểm đoạn thẳng AB. Tính độ dài đoạn thẳng DC.
Đáp án và Hướng dẫn giải
Bài 1.
Bài 2.
a) Ta có: AB + BC = 4 +3 = 7 (cm), AC = 6 cm.
Nên AB + BC ≠ AC. Vậy điểm B không nằm giữa A, C.
Ta có: AB + AC = 4 + 6 = 10 (cm), BC = 3 cm.
Nên AB + AC ≠ BC. Vậy điểm A không nằm giữa B, C.
Ta có: AC + BC = 6 + 3 = 9 (cm), AB = 4 cm.
Nên AC + BC ≠ AB. Vậy điểm C không nằm giữa A, B.
b) Trong ba điểm A, B, C không có điểm nào nằm giữa hai điểm còn lại.
Vậy ba điểm A, B, C không thẳng hàng.
Bài 3.
a) Trên tia Ax có B, C và AB < AC (vì 4 cm < 8 cm ), nên B nằm giữa A và C.
b) B nằm giữa A và C nên : AB + BC = AC
4 + BC = 8
BC = 8 – 4 = 4 (cm)
Ta có B nằm giữa A và C và AB = BC = 4 cm nên B là trung điểm của đoạn thẳng AC
c) D là trung điểm của đoạn thẳng AB nên:
D là trung điểm của AB; B nằm giữa A và C nên D nằm giữa A và C
Do đó: AD + DC = AC
2 + DC = 8
DC = 8 – 2 = 6 (cm)
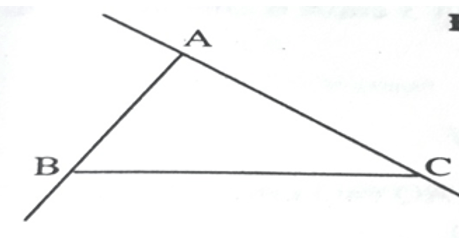
Đề kiểm tra 3:Bài 1. (4 điểm) Cho 3 điểm A, B , C không thẳng hàng. Hãy vẽ đoạn thẳng BC, tia AB và đường thẳng CA.
Bài 2. (6 điểm) Trên tia Ox lấy hai điểm A, B sao cho OA = 3 cm, OB = 7 cm
a) Tính AB
b) Gọi C là trung điểm AB. Tính AC
Đáp án và Hướng dẫn giải
Bài 1.
Bài 2.
a) Trên tia Ox có A, B và OA < OB (vì 3 cm < 7 cm ), nên A nằm giữa O và B
Do đó OA + AB = OB
3 + AB = 7
AB = 7 – 3 = 4 (cm)
b) C là trung điểm của đoạn thẳng AB
Bài 1. (2 điểm) Trên đường thẳng d lấy ba điểm E, Q, S theo thứ tự đó.
a) Hỏi có mấy đoạn thẳng tất cả, hãy kể tên các đoạn thẳng đó
b) Viết tên hai tia đối nhau gốc Q.
Bài 2. (2 điểm) Cho trước 4 điểm A, B, C, D trong đó không có 3 điểm nào thẳng hàng. Tìm điểm E sao cho A, E, B thẳng hàng và C, E, D thẳng hàng.
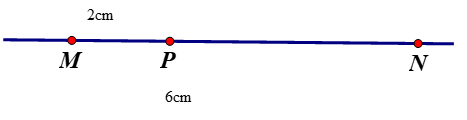
Bài 3. (3 điểm) Cho ba điểm M, N, P thẳng hàng, điểm M không nằm giữa hai điểm N và P. Biết: MN = 6 cm, MP = 2 cm. Tính PN.
Bài 4. (3 điểm) Trên tia Ox, vẽ hai điểm A, B sao cho OA = 3 cm, OB = 6 cm.
a) So sánh OA và AB.
b) Điểm A có là trung điểm của đoạn thẳng OB không? Vì sao ?
Đáp án và Hướng dẫn giải
Bài 1.
a) Có 3 đoạn thẳng đó là: RQ, QS, RS
b) Hai tia đối nhau gốc Q là: tia QR và tia QS
Bài 2.
Vẽ hai đường thẳng AB và CD cắt nhau tại E
Điểm E là điểm cần tìm
Trường hợp AB và CD không cắt nhau thì không tìm được điểm E
Bài 3.
Nếu điểm N nằm giữa hai điểm M, P thì:
MN + NP = MP
6 + NP = 2 (vô lí)
Do vậy N không nằm giữa M, P. Theo đề bài thì M không nằm giữa N và P và M, N, P thẳng hàng. Vậy P nằm giữa M và N.
⇒ MP + PN = MN
⇒ PN = MN – MP = 6 – 2 = 4 (cm)
Bài 4.
a) Trên tia Ox có A, B và OA < OB (vì 3 cm < 6 cm ), nên A nằm giữa O và B
Do đó OA + AB = OB
3 + AB = 6
AB = 6 – 3 = 3 (cm)
Vậy: OA = AB = 3 (cm)
b) Điểm A nằm giữa O, B và OA = AB. Vậy A là trung điểm của đoạn thẳng OB

Bài 1:
UCLN(252;540)=36
Bài 2: b=6; a=4
Bài 5:
Số chữ số có 1 chữ số là (9-1+1)x1=9(chữ số)
Số chữ số có 2 chữ số là (99-10+1)x2=180(chữ số)
Số chữ số có 3 chữ số là (132-100+1)x3=99(chữ số)
Số chữ số cần dùng là:
9+180+99=288(chữ số)
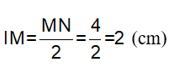

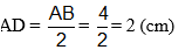

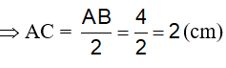


Ta có :
\(a+3⋮2a+1\)
\(\Leftrightarrow2\left(a+3\right)⋮2a+1\)
\(\Leftrightarrow2a+6⋮2a+1\)
\(\Leftrightarrow2a+1+5⋮2a+1\)
\(\Leftrightarrow5⋮2a+1\)
\(\Leftrightarrow2a+1\inƯ\left(5\right)\)
\(\Leftrightarrow2a+1\in\left\{1;-1;5;-5\right\}\)
\(\Leftrightarrow2a\in\left\{0;-2;4;-6\right\}\)
\(\Leftrightarrow a\in\left\{0;-1;2;-3\right\}\)
Mà \(a\in N\)
\(\Rightarrow a\in\left\{0;2\right\}\)
Vậy \(a\in\left\{0;2\right\}\)
Chúc bạn học tốt !!!
Giả sử : a+3 : 2a+1 Dấu : là chia hết nhé . Nhớ k
suy ra 2a+1 : 2a+1
Ta có :
2a+1 : 2a+1 <1>
a+3 : 2a+1 suy ra 2[a+3] : 2a+1 suy ra 2a+6 : 2a+1 <2>
Từ <1> và <2> suy ra [{2a+6} - {2a+1}] :2a+1
suy ra 5:[2a+1]
Suy ra 2a+1 e Ư[5]
suy ra 2a+1 e [1,5]
*2a+1 = 5
suy ra a=2
*2a+1 = 1
suy ra a=0
Vậy a= 0 hoặc a= 2 thì a+3 chia hết cho 2a+1