H2
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
0
MM
0
TP
0
PT
1
CM
20 tháng 1 2018
Ta có:
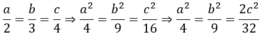
Theo tính chất dãy tỉ số bằng nhau ta có:
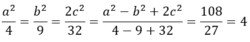
Ta có:
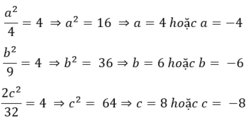
Mà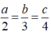 
nên a, b và c cùng dấu.
Vậy ta tìm được các số a1 = 4; b1 = 6; c1 = 8 hoặc a2 = -4; b2 = -6 và c2 = -8
PT
1
CM
7 tháng 6 2017
Ta có: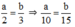 
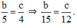
Suy ra: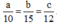 
Theo tính chất dãy tỉ số bằng nhau ta có: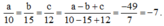 
Ta có:
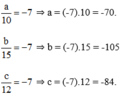
Vậy a = -70; b = -105; c = -84.
24 tháng 4 2016
Mình sẽ góp 1 cách (khá độc đáo...vì chẳng ai làm kiểu này cho tốn công), cũng khá nhanh
Có G(x)=x3−(a+b+c)x2+(ab+bc+ca)x−abcG(x)=x3−(a+b+c)x2+(ab+bc+ca)x−abc nhận a, b, c là nghiệm, thay x lần lượt bằng a, b, c xong cộng theo vế:
a3+b3+c3−3abc−...=0=>a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ca)a3+b3+c3−3abc−...=0=>a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ca)
24 tháng 4 2016
Cách thông dụng nhất:
a3+b3+c3−3abca3+b3+c3−3abc
=a3+3ab(a+b)+b3+c3−3abc−3ab(a+b)=a3+3ab(a+b)+b3+c3−3abc−3ab(a+b)
=(a+b)3+c3−3ab(a+b+c)=(a+b)3+c3−3ab(a+b+c)
=(a+b+c)(a2+2ab+b2−ab−ac+c2)−3ab(a+b+c)=(a+b+c)(a2+2ab+b2−ab−ac+c2)−3ab(a+b+c)
=(a+b+c)(a2+b2+c2−ab−bc−ca)=(a+b+c)(a2+b2+c2−ab−bc−ca)
_____
P/s: Mình đang nghĩ thêm cách nữa, nếu được sẽ post lên.
NS
0
a,b,c là số nguyên dương => 3abc>0
=> a3-b3-c3>0 => a3>b3 => a>b và a3>c3 => a>c
=> 2a > b+c => 4a > 2(b+c)
=> 4a>a2 => a<4
Mà 2(b+c) là số chẵn => a2 chẵn hay a chẵn => a=2
Vì b,c<2 và b,c thuộc Z+ => b=c=1
Vậy a=2,b=c=1