NH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LN
1
20 tháng 2 2020
a) \(ab+2a-b=7\)
<=> \(a\left(b+2\right)-\left(b+2\right)=5\)
<=> \(\left(a-1\right)\left(b+2\right)=5\)
| a-1 | -5 | -1 | 1 | 5 |
| b+2 | -1 | -5 | 5 | 1 |
| a | -4 | 0 | 2 | 6 |
| b | -3 | -7 | 3 | -1 |
| tm | tm | tm | tm |
Vậy có các cặp số nguyên ( a; b ) \(\in\){ ( -4; -3) , ( 0; -7) , ( 2; 3) , ( 6; -1) }
b) \(ab-2a+3b=-5\)
<=> \(\left(ab-2a\right)+\left(3b-6\right)=-5-6\)
<=> \(a\left(b-2\right)+3\left(b-2\right)=-11\)
<=> \(\left(b-2\right)\left(a+3\right)=-11\)
Kẻ bảng rồi làm. Hoặc chia các trường hợp
c) \(2ab-3a+b=10\)
<=> \(4ab-6a+2b=20\)( nhân cả hai vế với 2)
<=> \(2a\left(2b-3\right)+\left(2b-3\right)=20-3\)
<=> \(\left(2a+1\right)\left(2b-3\right)=17\)
Làm tiếp ....
NT
0
30 tháng 12 2017
a) (x+1)+(x+2)+(x+3)+........+(x+100)=5750
(x+x+...+x)+(1+2+3+...+100)=5750
(x.100)+(1+100).100:2=5750
(x.100)+5050=5750
x.100=5750-5050
x.100=700
x =700:100
x = 7
Vậy x = 7
c) trước hết cần chú ý rằng mọi số tự nhiên đều viết được dưới 1 trong 3 dạng: 3k, 3k +1 hoặc 3k +2(với k là số tự nhiên)
+) Nếu p = 3k vì p là số nguyên tố nên k = 1 => p = 3 => p+10 = 13 là số nguyên tố; p+14 = 17 là số nguyên tố (1)
+) Nếu p = 3k +1 => p +14 = 3k+1+14 = 3k+15 = 3(k+5) chia hết cho 3 và lớn hơn 3 nên là hợp số (loại vì không thỏa mãn điều kiện đề bài) (2)
+) Nếu p=3k+2 => p+10 = 3k+2+10 = 3k+12 = 3(k+4) chia hết cho 3 và lớn hơn 3 nên là hợp số (loại vì không thỏa mẫn điều kiện đề bài) (3)
Từ (1), (2), (3) suy ra p = 3 là giá trị cần tìm.
Vậy nha còn câu b mình tạm thời chưa biết, chúc bạn học tốt
29 tháng 4 2018
ab+2a-b=3
a(b+2)-b=3
a(b+2)-b+2=3+2
(b+2)(a-1)=5
sau đó bạn tìm các nghiệm cho chúng thỏa mãn nhé(cho là hai số trên thuộc ước của 5 rồi tính)
14 tháng 2 2018
Ta có :
\(ab+2a-b=3\)
\(\Leftrightarrow\)\(a\left(b+2\right)-b-2=1\)
\(\Leftrightarrow\)\(a\left(b+2\right)-\left(b+2\right)=1\)
\(\Leftrightarrow\)\(\left(a-1\right)\left(b+2\right)=1\)
Đến đây bạn xét các trường hợp ra
Chúc bạn học tốt
AH
Akai Haruma
Giáo viên
22 tháng 12 2022
Lời giải:
$ab+11=2a+3b$
$ab-2a-3b+11=0$
$a(b-2)-3(b-2)+5=0$
$(a-3)(b-2)=-5$
Vì $a,b$ là số nguyên nên $a-3, b-2$ là số nguyên. Ta có bảng sau: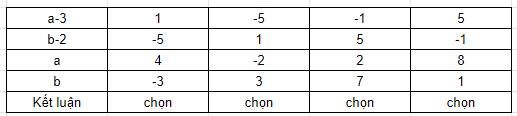
LN
0
VP
1
HN
20 tháng 2 2018
=> ab - 2a + 3b = 0-1 =-1
a(b - 2) + 3b = -1
a(b -2) + 3b - 6+ 6 = -1
a(b - 2) + 3b - 3 . 2 = -1 - 6= -7
a(b - 2) + 3(b - 2) = -7
(b -2) (a + 3) = -7
Có -7 = (-1). 7 = (-7) . 1
=> +) b - 2= -1 và a + 3 = 7
+) b - 2 = -7 và a + 3 = 1
lập bảng :
| b+2 | -1 | -7 |
| b | -3 | -9 |
| a+3 | 7 | 1 |
| a | 4 | -2 |
vậy: +) b = -3 và a = 4
+) b = -9 và a = -2
HP
26 tháng 3 2016
đơn giản
ab+2a-(b+2)=1
<=>a(b+2)-(b+2)=1
<=>(a-1)(b+2)=1=1.1=(-1).(-1)
+)(a-1)(b+2)=1.1
=>a-1=1 và b+2=1
=>a=2 và b=-1
+)(a-1)(b+2)=(-1).(-1)
=>a-1=-1 và b+2=-1
=>a=0 và b=-3
Vậy \(\left(a;b\right)\in\left\{\left(0;-3\right);\left(2;-1\right)\right\}\)
