Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
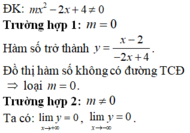
Suy ra đồ thị hàm số có 1 đường TCN y = 0.
Do đó đồ thị hàm số có đúng 2 đường tiệm cận đồ thị hàm số có đứng 1 đường tiệm cận đứng phương trình m x 2 - 2 x + 4 = 0 có nghiệm kép hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm x = 2.
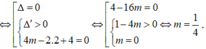
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A
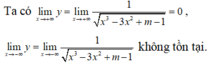
Suy ra y = 0 là đường tiệm cận ngang của đồ thị hàm số.
Do đó, để đồ thị hàm số đã cho có 4 đường thẳng tiệm cận thì phương trình x 3 - 3 x 2 + m - 1 = 0 có 3 nghiệm phân biệt
Chọn A
Chọn A.
Ta có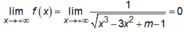 
nên đồ thị hàm số có một đường tiệm cận ngang y = 0.
nên không tồn tại giới hạn
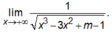
Do vậy đồ thị hàm số chỉ có một tiệm cận ngang y = 0.
Để đồ thị hàm số có bốn đường tiệm cận thì phương trình 
(1) có ba nghiệm phân biệt.
Số nghiệm của (2) là giao điểm của đường thẳng y = 1 –m và đồ thị hàm số 
Xét hàm số 
Ta có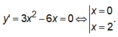 
Bảng biến thiên
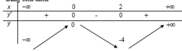
Dựa vào bảng biến thiên, ta thấy (2) có ba nghiệm phân biệt ⇔ -4 < 1-m < 0 ⇔ 1 < m < 5
Với \(m=0\) ko thỏa mãn
Với \(m\ne0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=-\dfrac{1}{\sqrt{m}}\); \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) Hàm có 2 TCN khi \(\sqrt{m}\) xác định \(\Rightarrow m>0\)
Lời giải:
Theo đề thì cần tìm $m$ để đths đã cho cho TCĐ $x=2$
Điều này xảy ra khi mà $2x+2m=0$ tại $x=2$
$\Leftrightarrow m=-x=-2$
Đáp án B.
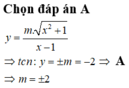
Đáp án A