
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có : 3a65b chia hết cho 5
Thì b chỉ có thể bằng 0;5
Th1: b = 0 thì (3 + a + 6 + 5 + 0) chia hết cho 9
=> (14 + a) chia hết cho 9
=> a = 4
Th2: b =5 thì (3 + a + 6 + 5 + 5) chia hết cho 9
=> 19 + a chia hết cho 9
=> a = 8

Bài 9:
a) Ta thấy nếu như muốn chia hết cho 2 và 5 thì số tận cùng là 0. Vậy thay b bằng 0 để được số 24a0. Còn chia hết cho 3 và 9 thì a có thể là số 3.
b) 28320 hoặc 28350.

Dấu hiệu chia hết cho 5 : các chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5
Vậy b có thể bằng 0 hoặc 5
Dấu hiệu chia hết cho 9 : tổng các chữ số đó cộng lại chia hết cho 9 thì số đó chia hết cho 9
4 + 8 + 7 + 0 = 19 ( ko chia hết cho 9 )
Vậy a chỉ có thể bằng 8
Vậy b = 0
b = 0 cũng chia hết cho 2
Số cần tìm là 848700
Những số chia hết cho \(2\) và \(5\) là những số có tận cùng là những số có tận cùng là \(0\) vì \(2\times5=10\) và những số chia hết cho \(10\) là những số có tận cùng là \(0\)
Từ đó ta dễ biết \(b=0\)
Ta có: \(\overline{a48700}=a+4+8+7+0+0=19\)
Ma những số chia hết cho \(9\) là những số có tổng các chữ số chia hết cho \(9\)
Mà \(27\) chia hết cho \(9\) nên \(a=27-19=8\)
Vậy \(a=8\)
Vậy số \(\overline{a4870b}=848700\) để chia hết cho \(2;5\) và \(9\)
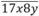 chia hết cho cả 5 và 9.
chia hết cho cả 5 và 9.
a=9,b=0
nhớ **** cho mình nha các bạn