PN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KN
14 tháng 2 2020
We put \(n^2-14n+38=k^2\)
\(\Rightarrow n^2-14n+49-11=k^2\)
\(\Rightarrow\left(n-7\right)^2-11=k^2\)
\(\Rightarrow\left(n-7\right)^2-k^2=11\)
\(\Rightarrow\left(n-7-k\right)\left(n-7+k\right)=11=1.11=11.1=\left(-1\right).\left(-11\right)\)
\(=\left(-11\right).\left(-1\right)\)
Prints:
| \(n-7-k\) | \(1\) | \(11\) | \(-11\) | \(-1\) |
| \(n-7+k\) | \(11\) | \(1\) | \(-1\) | \(-11\) |
| \(n-k\) | \(8\) | \(18\) | \(-4\) | \(6\) |
| \(n+k\) | \(18\) | \(8\) | \(6\) | \(-4\) |
Case by case, we have \(n\in\left\{13;1\right\}\)
20 tháng 7 2021
b)
https://hoc24.vn/cau-hoi/c-voi-a-b-c-la-cac-so-duong-thoa-man-dieu-kien-a-b-c-2-tim-max-q-sqrt2abcsqrt2bcasqrt2cab.8298826302
Bạn có thể tham khảo ở đây. Đừng quên like giúp mik nha bạn. Thx
28 tháng 12 2019
\(\left(a-\sqrt{2011}\right)\left(b+\sqrt{2011}\right)=14\)
\(\Leftrightarrow ab+\sqrt{2011}\left(a-b\right)=2025\)
Có: a,b nguyên => a-b nguyên
=> VP=VT <=> \(\sqrt{2011}\left(a-b\right)\)nguyên
=> a-b=0 <=> a=b
=> pt <=> a^2=2025
Làm nốt nhé.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
\(b+c\le\sqrt{2\left(b^2+c^2\right)}\Rightarrow\dfrac{a^2}{b+c}\ge\dfrac{a^2}{\sqrt{2\left(b^2+c^2\right)}}=\dfrac{1}{\sqrt{2}}.\dfrac{a^2}{\sqrt{b^2+c^2}}\)
Sau đó làm tiếp như bài đó là được
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
\(P\sqrt{2}\ge\dfrac{a^2}{\sqrt{b^2+c^2}}+\dfrac{b^2}{\sqrt{c^2+a^2}}+\dfrac{c^2}{\sqrt{a^2+b^2}}\)
Đặt \(\left(\sqrt{b^2+c^2};\sqrt{c^2+a^2};\sqrt{a^2+b^2}\right)=\left(x;y;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=\sqrt{2011}\\a^2=\dfrac{y^2+z^2-x^2}{2}\\b^2=\dfrac{z^2+x^2-y^2}{2}\\c^2=\dfrac{x^2+y^2-z^2}{2}\end{matrix}\right.\)
\(\Rightarrow P2\sqrt{2}\ge\dfrac{y^2+z^2-x^2}{x}+\dfrac{z^2+x^2-y^2}{y}+\dfrac{x^2+y^2-z^2}{z}\)
\(P4\sqrt{2}\ge\dfrac{\left(y+z\right)^2}{2x}+\dfrac{\left(z+x\right)^2}{2y}+\dfrac{\left(x+y\right)^2}{2z}-\left(x+y+z\right)\)
\(P2\sqrt{2}\ge\dfrac{4\left(x+y+z\right)^2}{2\left(x+y+z\right)}-\left(x+y+z\right)=x+y+z=\sqrt{2011}\)
\(\Rightarrow P\ge\dfrac{\sqrt{2011}}{2\sqrt{2}}\)
Đề sai
TN
17 tháng 5 2016
ta có:
\(x\left(\sqrt{2011}+\sqrt{2010}\right)+y\left(\sqrt{2011}-\sqrt{2010}\right)=x\sqrt{2011}+x\sqrt{2010}+y\sqrt{2011}-y\sqrt{2010}\)
pt tương đương với:
\(\left(x+y\right)\sqrt{2011}+\left(x-y\right)\sqrt{2010}=\sqrt{2011^3}+\sqrt{2010^3}\)
vì x,y là số hữu tỉ nên
\(\hept{\begin{cases}\sqrt{2011}\left(x+y\right)=\sqrt{2011^3}\\\sqrt{2010}\left(x-y\right)=\sqrt{2010^3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x+y=2011\\x-y=2010\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{4021}{2}\\y=\frac{1}{2}\end{cases}}\)
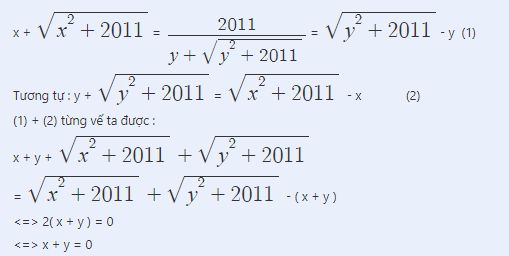
ĐK: \(\hept{\begin{cases}a\ge0\\b\ge0\\a+b\ge2011\end{cases}}\)
pt => \(a+b-2011=a+b+2011-2\sqrt{2011}\left(\sqrt{a}+\sqrt{b}\right)+2\left(\sqrt{ab}\right)\)
<=> \(2.2011-2\sqrt{2011}.\sqrt{a}-2\sqrt{2011}\sqrt{b}+2\sqrt{ab}=0\)
<=> \(\sqrt{2011}\left(\sqrt{2011}-\sqrt{a}\right)-\sqrt{b}\left(\sqrt{2011}-\sqrt{a}\right)=0\)
<=> \(\left(\sqrt{2011}-\sqrt{a}\right)\left(\sqrt{2011}-\sqrt{b}\right)=0\)
<=> a = 2011 và b = 2011 ( thỏa mãn đk )
Thử lại với phương trình ta thấy thỏa mãn
Vậy a= b = 2011.