Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 3 cạnh tam giác vuông là (n-1), n và (n+1), ta có:
(n-1)2 + n2 = (n+1)2
n2 -2n + 1 + n2 = n2 + 2n + 1
n2 - 4n =0
n(n-4) = 0
n = 0 (loại) hoặc n=4
Vậy 3 cạnh là: 3, 4, 5

\(B_2=\left\{x;x=2k,k\in N\right\}\)
\(B_4=\left\{x;x=4m,m\in N\right\}\)
Do \(4m=2.\left(2m\right)\Rightarrow B_4\subset B_2\)
\(\Rightarrow B_2\cap B_4=B_4\)

*: Gọi số thứ nhất là a; số thứ hai là b
Ta có a+b=27
Vì a chia hết cho 3;b chia hết cho 3
=>a có dạng 3k;b có dạng 3n(n;k EN/ƯCLN(n;k)=1)
=>3k+3n=27
3*(k+n)=27
(k+n)=27:3
(k+n)=9
Ta có bảng giá trị sau:
| k | n | a | b |
| 1 | 8 | 3 | 24(loại vì BCNN=24) |
| 2 | 7 | 6 | 21(loại vì BCNN=42) |
| 4 | 5 | 12 | 15(thỏa) |
| 5 | 4 | 15 | 12(thỏa) |
| 7 | 2 | 21 | 6(loại) |
| 8 | 1 | 24 | 3(loại) |
Vậy hai số cần tìm là 12 và 15
*:đang nghĩ

Đáp án A
Mệnh đề P: “Ba số tự nhiên là ba số tự nhiên liên tiếp”.
Mệnh đề Q: “Ba số tự nhiên có tổng chia hết cho 3”.
Khi đó, Q=>P được phát biểu là:
“Nếu ba số tự nhiên có tổng chia hết cho 3 thì ba số tự nhiên đó là ba số tự nhiên liên tiếp”.
Nói gọn: “Ba số tự nhiên có tổng chia hết cho 3 thì liên tiếp”.


gọi các số cần tìm là n, thương của phép chia n là cho 9 là abc
theo bài ra ta có: n= 9.abc = 9.(a.100+b.10+c)= a.900+b.90+c.9
=> n>a.900 mà a> 1 => a.900>900
=> n>a.900>900
=> n>900
vì n chia hết cho 9 và 5 mà (9,5)=1
=> n chia hết cho 45
=> n=45.k
mà 900<n<1000 => 900< 45.k<1000 => 20<k<23
=> k = 21,22
=> n= 45.k = 945,990
vậy các số cần tìm là 945,990

Gọi số cần tìm là ab (gạch ngang trên đầu)
Ta có: aabb - ab = 1180
1100a + 11b - 10a - b = 1180
1090a + 10b = 1180
a khác 0 thõa mãn ab có 2 chữ số
Nếu a > 1 < = > a \(\ge\) 2 thì 1090a > 1180 => Không tìm được
0 < a < 2 => a= 1
Ta có: 1090 + 10b = 1180
10b = 1180 - 1090 = 90
< = > b = 90 : 10 = 9
Vậy ab = 19
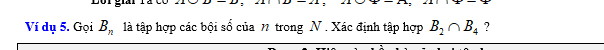

Dễ:
Gọi 3 số tự nhiên liên tiếp cần tìm là:
a;a+1;a+2
Theo bài ra ta có:
a+a+1+a+2=27
a.3+3=27
a.3=27-3
a.3=24
a=24:3
a=8.
Vậy 3 số tự nhiên liên tiếp đó là:
8;9;10.
ukm bài này đúng rồi nhưng lần sau bạn trình bày bằng fx sẽ đẹp hơn nhé!