K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
NT
1
14 tháng 2 2020
Theo bài ra, ta có : \(\hept{\begin{cases}\left(a,b\right)=36\\\left[a,b\right]=720\\a+36=b\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}ab=\left(a,b\right).\left[a,b\right]=36.720=25920\\b-a=36\end{cases}}\)nên a<b
Vì (a,b)=36 nên ta có : \(\hept{\begin{cases}a=36m\\b=36n\\\left(m,n\right)=1;m< n\end{cases}}\)
Mà ab=25920
\(\Rightarrow\)36m.36n=25920
\(\Rightarrow\)1296m.n=25920
\(\Rightarrow\)mn=20
Vì (m,n)=1 ; b-a=36 và m<n nên ta có bảng sau :
m 4
n 5
a 144
b 180
Vậy a=144 và b=180.
LB
0
5 tháng 12 2019
Vì UClN (a,b)=3
=> a=3k ; b=3q (k và q nguyên tố cùng nhau,; k, q là số tự nhiên khác 0)
=> a x b =3 k x 3q= 9 x k x q
mà a x b =36
=> k x q =4
mà k và q nguyên tố cùng nhau,; k, q là số tự nhiên khác 0
TH1: k=1 ;q=4 => a=3;b=12
TH2: k=4;q=1 => a=12;b=3
XO
5 tháng 12 2019
Vì ƯCLN(a;b) = 3
=> Đặt \(\hept{\begin{cases}a=3m\\b=3n\end{cases}\left(m;n\right)=1;\left(m;n\inℕ^∗\right)}\)
Khi đó a.b = 36
<=> 3m.3n = 36
=> m.n = 4
Với \(m;n\inℕ^∗;\left(m;n\right)=1\)có : 4 = 1.4
Lập bảng xét các trường hợp :
| m | 1 | 4 |
| n | 4 | 1 |
| a | 3 | 12 |
| b | 12 | 3 |
Vậy các cặp (a;b) thỏa mãn là (12 ; 3) ; (3; 12)
PT
1
TK
3
DL
10 tháng 11 2017
Tương tự thôi
a.b = 48
Giả sử a >b
a = 2m ; b = 2n
m > n ; ( m,n) = 1 (ƯCLN(m,n) =1 )
a . b = 2m . 2n
=4.mn
m.n = 48 : 4
m.n = 12
Lập bảng ra
Vì dụ vì ƯCLN ( m,n) = 1 nên m = 4 ; n = 3
=> a = 12 ; b = 9
DL
10 tháng 11 2017
Giả sử a > b
a = 3m ; b = 3n
m > n ; (m,n) = 1
3m . 3n = a.b
9.m.n=36
m.n = 4
Bạn lập bảng ra là được :
Vì ƯCLN(m,n) = 1 suy ra ....
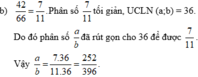
Câu đúng là Tìm ab biết a+b=216 và ƯCLN(a;b)