Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Để hàm số trên liên tục tại $x_0=0$ thì:
\(\lim\limits_{x\to 0+}f(x)=\lim\limits_{x\to 0-}f(x)=f(0)\)
\(\Leftrightarrow \lim\limits_{x\to 0+}(a+\frac{4-x}{x+2})=\lim\limits_{x\to 0-}(\frac{\sqrt{1-x}+\sqrt{1+x}}{x})=a+2\)
\(\Leftrightarrow a+2=\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}\)
Mà \(\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}=-\infty \) nên không tồn tại $a$ để hàm số liên tục tại $x_0=0$

2.
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+2a\right)=2a\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\left(x^2+x+1\right)=1\)
Hàm liên tục tại \(x=0\Leftrightarrow\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)\)
\(\Leftrightarrow2a=1\Rightarrow a=\dfrac{1}{2}\)
3. Đặt \(f\left(x\right)=x^4-x-2\)
Hàm \(f\left(x\right)\) liên tục trên R nên liên tục trên \(\left(1;2\right)\)
\(f\left(1\right)=-2\) ; \(f\left(2\right)=12\Rightarrow f\left(1\right).f\left(2\right)=-24< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (1;2)
Hay pt đã cho luôn có nghiệm thuộc (1;2)

\(\lim\limits_{x\rightarrow0}f\left(x\right)=\lim\limits_{x\rightarrow0}\dfrac{2\sqrt{x+1}-x-2}{x^2}=\lim\limits_{x\rightarrow0}\dfrac{\left(2\sqrt{x+1}\right)^2-\left(x+2\right)^2}{x^2\left(2\sqrt{x+1}+x+2\right)}=\lim\limits_{x\rightarrow0}\dfrac{4x+4-x^2-4x-4}{x^2\left(2\sqrt{x+1}+x+2\right)}=\lim\limits_{x\rightarrow0}\dfrac{-1}{2\sqrt{x+1}+x+2}=-\dfrac{1}{4}\)
\(f\left(0\right)=2-9m\)
De ham so lien tuc tai x=0
\(\Rightarrow f\left(0\right)=\lim\limits_{x\rightarrow0}f\left(x\right)\Leftrightarrow2-9m=-\dfrac{1}{4}\Rightarrow m=\dfrac{1}{4}\)
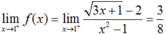
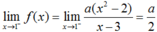
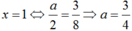
- Ta có:
→ Hàm số không liên tục tại x = 0.
Chọn C.