Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề ra ta có:
\(\frac{8a}{7}=\frac{8b}{9}=\frac{5c}{7}hay\frac{a}{\frac{7}{8}}=\frac{b}{\frac{9}{8}}=\frac{c}{\frac{7}{5}}\)
và \(a-b=20\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{\frac{7}{8}}=\frac{b}{\frac{9}{8}}=\frac{c}{\frac{7}{5}}=\frac{a-b}{\frac{7}{8}-\frac{9}{8}}=\frac{20}{\frac{-1}{4}}=-80\)
\(\rightarrow a=-80\cdot\frac{7}{8}=-70\)
\(\rightarrow b=-80\cdot\frac{9}{8}=-90\)
\(\rightarrow c=-80\cdot\frac{7}{5}=-112\)

Ta có: a.8/7 = b.8/9 = c.5/7
=> \(\frac{a}{\frac{7}{8}}=\frac{b}{\frac{9}{8}}=\frac{c}{\frac{7}{5}}=\frac{b-a}{\frac{9}{8}-\frac{7}{8}}=\frac{20}{\frac{1}{4}}=80\) (áp dụng tính chất của dãy tỉ số bằng nhau)
=> a = 80 x 7/8 = 70
=> b = 70 + 20 = 90
=> c = 80 x 7/5 = 112

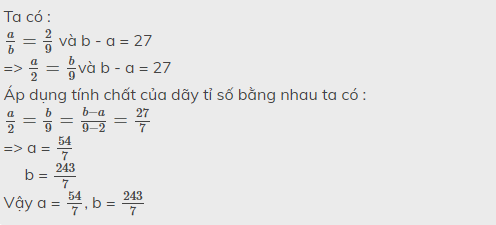
\(1,4a=5b\Leftrightarrow\dfrac{a}{5}=\dfrac{b}{4}=\dfrac{b-a}{4-5}=\dfrac{27}{-1}=-27\\ \Leftrightarrow\left\{{}\begin{matrix}a=-135\\b=-108\end{matrix}\right.\\ 2,\dfrac{1}{3}x=\dfrac{1}{2}y=\dfrac{1}{5}z\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{z}{5}=\dfrac{x+2y-z}{3+4-5}=\dfrac{8}{2}=4\\ \Leftrightarrow\left\{{}\begin{matrix}x=12\\y=8\\z=20\end{matrix}\right.\\ 3,\dfrac{1}{3}a=\dfrac{1}{2}b;\dfrac{1}{5}a=\dfrac{1}{7}c\\ \Leftrightarrow\dfrac{a}{15}=\dfrac{b}{10}=\dfrac{c}{21}=\dfrac{a+b+c}{15+10+21}=\dfrac{184}{46}=4\\ \Leftrightarrow\left\{{}\begin{matrix}a=60\\b=40\\c=84\end{matrix}\right.\)

a và b tỉ lệ thuận với 7 và 11 nên a/7 = b/11 <=> a/56=b/88 (1)
b và c tỉ lệ nghịch với 3 và 8 nên 3b=8c <=> b/8 = c/3 <=> b/88 = c/33 (2)
Từ (1) và (2) suy ra a/56=b/88=c/33
Hay 5a/280=3b/264=2c/66 và 5a - 3b + 2c = 164
Vậy 5a/280=3b/264=2c/66 = (5a-3b+2c)/(280-264+66) = 164/82 = 2
Do đó:
a=2.56=112
b=2.88=176
c=2.33=66
tk nha bạn
thank you bạn
(^_^)

Gọi a,b là 2 số cần tìm(a>b>0 và a,b thuộc Z)
Theo đề:a+b,a-b,ab tỉ lệ nghịch với 20,140,7
<=>20(a+b)=140(a-b)(1) và 140(a-b)=7ab (2)
Ta có:
(1)<=>20b+140b=140a-20a
<=>160b=120a
=>a=4/3.b thế vào (2) đc:
140(4/3b-b)=7.(4/3 b)b
<=>140/3.b=28/3.b²
<=>b=(140/3):(28/3)=5
=>a=4/3.5=20/3(loại vì a thuộc Z)
Vậy hok có a,b nào thỏa mãn điều kiện đề bài

Gọi 2 số cần tìm là x và y ta có:
\(20\left(x+y\right)=140\left(x-y\right)=7xy\)
\(\Rightarrow\frac{x+y}{7}=\frac{x-y}{1}=\frac{xy}{20}=\frac{x+y+x-y}{7+1}=\frac{x+y-x+y}{7-1}=\frac{x}{4}=\frac{y}{3}=\frac{xy}{4y}=\frac{xy}{3x}\)
\(3x=20\Rightarrow x=6\frac{2}{3};\) \(4y=20\Rightarrow y=5\)
Vậy các số cần tìm là \(6\frac{2}{3}\) và 5.

Theo đề bài, ta có:
\(\frac{a}{5}=\frac{b}{7}=\frac{c}{8}\) và \(a+b+c=40\)
áp dụng tính chất dãy tỉ số bằng nhau , ta có
\(\frac{a}{5}=\frac{b}{7}=\frac{c}{8}=\frac{a+b+c}{5+7+8}=\frac{40}{20}=2\)
\(a=2.5=10\)
\(b=2.7=14\)
\(c=2.8=16\)
theo đề ra ta có
\(\frac{a}{5}=\frac{b}{7}=\frac{c}{8};a+b+c=40\)
ÁP dụng tinbhs chất của dãy tỉ số bằng nhau , ta có
\(\frac{a}{5}=\frac{b}{7}=\frac{c}{8}=\frac{a+b+c}{5+7+8}=\frac{40}{20}=2\)
\(\Rightarrow a=2\cdot5=10\)
\(b=2\cdot7=14\)
\(c=2\cdot8=16\)
Vậy ...........................