Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phân số cần tìm là \(\frac{a}{a+22}\left(a\ne-22\right)\)
Theo bài ra, ta có: \(\frac{a+5}{a+22-2}=\frac{1}{2}\Rightarrow2\left(a+5\right)=a+20\)
\(\Leftrightarrow2a+10=a+20\Leftrightarrow2a-a=20-10\Leftrightarrow a=10\Rightarrow\frac{a}{a+22}=\frac{10}{10+22}=\frac{10}{32}\)
Vậy p/s đã cho là 10/32


Gọi tử ban đầu là \(x\left(x\ne-3\right)\)
Mẫu ban đầu là \(x+3\)(đây là lí do tại sao \(x\ne-3\))
Tử lúc sau là \(x+2\)
Mẫu lúc sau là \(x+3+2=x+5\)
Theo đề bài, ta có: \(\frac{x+2}{x+5}=\frac{1}{2}\)
Đến đây em tự giải nhé. (cũng dễ rồi)

Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
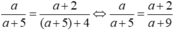
(Điều kiện: a ≠ - 5;a ≠ - 9 )
a(a + 9) = (a + 2)(a + 5)
⇔ a 2 + 9 a = a 2 + 7 a + 10
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10

Gọi tử là x
=>Mẫu là x+3
Theo đề, ta có: \(\dfrac{x+1}{x+4}=\dfrac{1}{2}\)
=>2x+2=x+4
=>x=2
=>Mẫu là 2+3=5
Gọi \(x,y\) lần lượt là tử số và mẫu số \(\left(x>0,y\ne0\right)\)
Theo đề bài, ta có hệ pt :
\(\left\{{}\begin{matrix}x+3=y\\\dfrac{x+1}{y+1}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=-3\\2x-y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\left(n\right)\\y=5\left(n\right)\end{matrix}\right.\)
Vậy tử số là 2, mẫu số là 5
Phân số cần tìm là \(\dfrac{2}{5}\)

Gọi tử số của phân số đó là \(x\left(x\in Z\right)\)
mẫu số của phân số đó là:\(x+3\)(do tử kém mẫu 3 đơn vị)
Vì thêm cả tử và mẫu của phân số đã cho 2 đơn vị thì ta được 1 phân số mới có giá trị bằng \(\frac{1}{2}\),nên ta có phương trình:
\(\frac{x+2}{\left(x+3\right)+2}=\frac{1}{2}\)
\(\Leftrightarrow\frac{x+2}{x+5}=\frac{1}{2}\)
\(\Leftrightarrow\frac{2\left(x+2\right)}{2\left(x+5\right)}=\frac{x+5}{2\left(x+5\right)}\)
\(\Leftrightarrow2x+4=x+5\)
\(\Leftrightarrow2x-x=5-4\)
\(\Leftrightarrow x=1\left(tm\right)\)
Vậy phân số đó là:\(\frac{1}{\left(1+3\right)}=\frac{1}{4}\)
Xong rồi đấy,bạn k cho mình nha