Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{15x}{7y^3}.\dfrac{2y^2}{x^2}=\dfrac{15x.2y^2}{7y^3.x^2}=\dfrac{30}{7xy}\)
b) \(\dfrac{4y^2}{11x^4}.\left(-\dfrac{3x^2}{8y}\right)=\dfrac{-4y^2.3x^2}{11x^4.8y}=\dfrac{-3y}{22x^2}\)
c) \(\dfrac{x^3-8}{5x+20}.\dfrac{x^2+4x}{x^2+2x+4}\\ =\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{5\left(x+4\right)}.\dfrac{x\left(x+4\right)}{x^2+2x+4}\\ =\dfrac{x^2-2x}{5}\)

`a)3x(2x^2-3x+4)`
`=6x^3-9x^2+12x`
______________________________________________
`b)(x+3)^2+(3x-2)(x+4)`
`=x^2+6x+9+3x^2+12x-2x-8`
`=4x^2+16x+1`
______________________________________________
`c)[2x-4]/[x-1]+[2x+2]/[x^2-1]` `ĐK: x \ne +-1`
`=[(2x-4)(x+1)+2x+2]/[(x-1)(x+1)]`
`=[2x^2+2x-4x-4+2x+2]/[(x-1)(x+1)]`
`=[2x^2-2]/[x^2-1]`
`=2`

a) Ta có: \(\dfrac{1-x}{x^2-2x+1}+\dfrac{x+1}{x-1}\)
\(=\dfrac{1-x}{\left(x-1\right)^2}-\dfrac{x+1}{1-x}\)
\(=\dfrac{1-x}{\left(1-x\right)^2}-\dfrac{x+1}{1-x}\)
\(=\dfrac{1-x-1}{1-x}=\dfrac{-x}{1-x}=\dfrac{x}{x-1}\)
b) Ta có: \(\dfrac{2x}{3y^4z}\cdot\left(-\dfrac{4y^2z}{5x}\right)\cdot\left(-\dfrac{15y^3}{8xz}\right)\)
\(=\dfrac{2x\cdot4y^2z\cdot15y^3}{3y^4z\cdot5x\cdot8xz}\)
\(=\dfrac{120xy^5z}{120x^2y^4z^2}=\dfrac{y}{xz}\)

a: \(=\dfrac{x+2y}{xy}\cdot\dfrac{2x^2}{\left(x+2y\right)^2}=\dfrac{2x}{y\left(x+2y\right)}\)
b: \(=\dfrac{x\left(4x^2-y^2\right)}{x^2+xy+y^2}\cdot\dfrac{\left(x-y\right)\left(x^2+xy+y^2\right)}{\left(2x-y\right)^3}\)
\(=\dfrac{x\left(x-y\right)\left(2x+y\right)\left(2x-y\right)}{\left(2x-y\right)^3}\)
\(=\dfrac{x\left(x-y\right)\left(2x+y\right)}{\left(2x-y\right)^2}\)
c: \(=\dfrac{x+3}{x+2}\cdot\dfrac{2x-1}{3\left(x+3\right)}\cdot\dfrac{2\left(x+2\right)}{2\left(2x-1\right)}\)
=1/3
d: \(=\dfrac{x+1}{x+2}:\left(\dfrac{1}{2x}\cdot\dfrac{3x+3}{2x-3}\right)\)
\(=\dfrac{x+1}{x+2}\cdot\dfrac{2x\left(2x-3\right)}{3\left(x+1\right)}=\dfrac{2x\left(2x-3\right)}{3\left(x+2\right)}\)

a: =2x^5-15x^3-x^2-2x^5-x^3=-16x^3-x^2
b: =x^3+3x^2-2x-3x^2-9x+6
=x^3-11x+6
c: \(=\dfrac{4x^3+2x^2-6x^2-3x-2x-1+5}{2x+1}\)
\(=2x^2-3x-1+\dfrac{5}{2x+1}\)
a) \(6x^3\left(\dfrac{1}{3}x^2-\dfrac{5}{2}-\dfrac{1}{6}\right)-2x^5-x^3\)
\(=6x^3\left(\dfrac{1}{3}x^2-\dfrac{16}{6}\right)-2x^5-x^3\)
\(=2x^5-16x^3-2x^5-x^3\)
\(=-17x^3\)
b) \(\left(x+3\right)\left(x^2+3x-2\right)\)
\(=x^3+3x^2-2x+3x^2+9x-6\)
\(=x^3+6x^2+7x-6\)
c) \(\left(4x^3-4x^2-5x+4\right):\left(2x+1\right)\)
\(=2x^2+4x^3-2x-4x^2-\dfrac{5}{2}-5x+\dfrac{2}{x}+4\)
\(=4x^3-2x^2-7x+\dfrac{2}{x}+\dfrac{3}{2}\)

a: \(=\left(x+2\right)^2\cdot\dfrac{2x-1}{3\left(x+2\right)}=\dfrac{\left(x+2\right)\left(2x-1\right)}{3}\)
b: \(=\dfrac{2\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-\left(x-2\right)}{x\left(x-1\right)}=\dfrac{-2\left(x+1\right)}{\left(x-1\right)\left(x+2\right)}\)

a, \(\dfrac{x^2+y^2}{4\left(x+y\right)}+\dfrac{2xy}{4\left(x+y\right)}\)=\(\dfrac{x^2+2xy+y^2}{4\left(x+y\right)}\) = \(\dfrac{\left(x+y\right)^2}{4\left(x+y\right)}\) =\(\dfrac{x+y}{4}\)
a. \(\dfrac{x^2+y^2}{4\left(x+y\right)}+\dfrac{2xy}{4\left(x+y\right)}\)
\(=\dfrac{x^2+2xy+y^2}{4\left(x+y\right)}\)
\(=\dfrac{\left(x+y\right)^2}{4\left(x+y\right)}\)
\(=\dfrac{x+y}{4}\)
b. \(\dfrac{x+5}{2x-2}-\dfrac{4}{x^2-1}:\dfrac{2}{x+1}\)
\(=\dfrac{x+5}{2\left(x-1\right)}-\dfrac{4}{\left(x+1\right)\left(x-1\right)}:\dfrac{2}{x+1}\)
\(=\dfrac{x+5}{2\left(x-1\right)}-\dfrac{2}{x-1}\)
\(=\dfrac{x+5}{2\left(x-1\right)}-\dfrac{4}{2\left(x-1\right)}\)
\(=\dfrac{x+1}{2\left(x-1\right)}\)
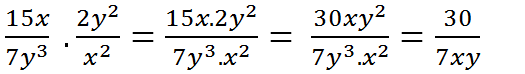
a) \(\dfrac{4y^2}{11x^4}:\left(-\dfrac{8y}{33x^2}\right)\)
\(=\dfrac{4y^2}{11x^4}.\left(-\dfrac{33x^2}{8y}\right)\)
\(=-\dfrac{4y^2.33x^2}{11x^4.8y}\)
\(=-\dfrac{3y}{2x^2}\)
b) \(\dfrac{x^2-4}{3x+12}.\dfrac{x+4}{2x-4}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{3\left(x+4\right)}.\dfrac{x+4}{2\left(x-2\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)\left(x+4\right)}{3\left(x+4\right).2\left(x-2\right)}\)
\(=\dfrac{x+2}{6}\).
\(\dfrac{\left(x-2\right)\left(x+2\right)\left(x+4\right)}{3\left(x+4\right).2\left(x-2\right)}=\dfrac{x+2}{6}\)