Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách giải:
Giải: Trong không khí vị trí vân sáng bậc 2 là: b 1 = 2 λ D a ; khoảng vân c 1 = λ D a
số vân sáng quan sát được trên màn là:
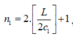
trong đó L là bề rộng trường giao thoa.
Làm thí nghiệm trên trong nước có chiết suất n > 1, với D,a và vị trí của S không đổi thì vị trí vân sáng bậc 2 là:
b
2
=
2
λ
D
n
a
; khoảng vân
c
1
=
λ
D
n
a
; số vân sáng quan sát được trên màn là:
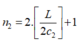
So sánh ta thấy: b1 > b2; c1 >c2; n1 < n2 => chọn B

Lúc đầu: \(\iota=\frac{\text{λ}D}{a}\)
Khi nhúng toàn bộ hệ thí nghiệm vào trong nước thì bước sóng ánh sáng sẽ giảm theo λ’ = λ/n, khi đó khoảng vân
\(\iota'=\frac{\text{λ}'D}{a}=\frac{\frac{\text{λ}}{n}D}{a}=\frac{1}{n}.\frac{\text{λ}D}{a}\)\(=\frac{1}{\frac{4}{3}}.\frac{0,6.10^{-6}.2}{3.10^{-3}}=0,3.10^{-3}m=0,3mm\)
---> chọn C

Chọn D.
Vận tốc ánh sáng trong không khí là c, bước sóng λ, khi ánh sáng truyền từ không khí vào nước thì tần số của ánh sáng không thay đổi, vận tốc ánh sáng truyền trong nước là v = c/n, n là chiết suất của nước. Khi đó bước sóng ánh sáng trong nước là λ’ = v/f = c/nf = λ/n. Khoảng vân quan sát được trên màn quan sát khi toàn bộ thí nghiệm đặt trong nước là i = λ ' D a = λD n . a = 0,3mm.

Chọn C
Khi khoảng cách từ màn quan sát đến mặt phẳng 2 khe là D + ΔD thì khoảng vân là:
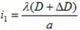
Khi khoảng cách từ màn quan sát đến mặt phẳng hai khe là D - ΔD thì khoảng vân là:
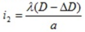
lại có:
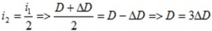
=> Nếu khoảng cách từ màn quan sát đến mặt phẳng hai khe là D + 3ΔD thì khoảng vân trên màn là:
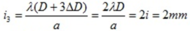
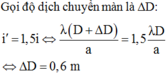
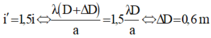
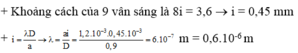


Đáp án D
Nhúng toàn bộ thí nghiệm vào trong nước thì khoảng vân quan sát được nhỏ hơn i.