Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A

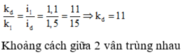

=>![]()
Hai vân trùng nhau chúng ta quan sát được sẽ không còn màu đỏ (hoặc lục) nên tổng số vân màu đỏ quan sát được trên MN là:
N do= 22-2=20

Số vân sáng màu đỏ trên đoạn MN là số các giá trị k1 nguyên thỏa mãn điều kiện
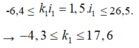
Có 22 giá trị k1 thỏa mãn điều kiện → có 22 vân sáng đỏ.
+ Xác định số vân trùng:
Vị trí vân trùng
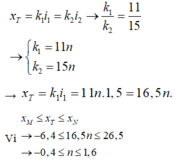
Có 2 giá trị n nguyên → có 2 vân trùng trong khoảng MN.
→ Số vân sáng màu đỏ thực tế quan sát được là 22 – 2 = 20 vân sáng.
Đáp án C

Phương pháp:
Sử dụng lí thuyết về bài toán trùng nhau của 2 bức xạ trong giao thoa sóng ánh sáng
Hai bức xạ trùng nhau: x1 = x2 <=> k1.λ1 = k2.λ2
Cách giải:
+ Ta có: i1 = 0,6 mm và i2 = 0,78 mm
+ Vị trí hai bức xạ trùng nhau:
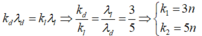

+ Số vân sáng của λ 1 = 500 nm trên đoạn MN là:
![]()
có 10 giá trị
+ Số vân sáng của λ 2 = 650 nm trên đoạn MN là:
![]()
có 8 giá trị
+ Số vân sáng trùng của hai bức xạ trên đoạn MN là:
![]()
có 1 giá trị
+ Số vân sáng quan sát được là: N = N1 + N2 – N0 = 17
Chọn B

Đáp án B
+ Khoảng vân giao thoa của các ánh sáng đơn sắc

+ Ta xét các tỉ số:
x M i 1 = 3 , 3 x M i 1 = 13 , 3 → trên đoạn MN có các vị trí cho vân sáng từ bậc 4 đến bậc 13 của bức xạ λ1
x M i 2 = 2 , 56 x M i 2 = 10 , 25 → trên đoạn MN có các vị trí cho vân sáng từ bậc 3 đến bậc 10 của bức xạ λ2
+ Điều kiện trùng nhau của hai hệ vân
λ 1 λ 2 = k 2 k 1 = 10 13 → trên đoạn MN có một vị trí trùng nhau của hệ hai vân sáng, do đó số vân sáng quan sát được là
n
=
10
+
8
-
1
=
17
(ta trừ một là do hai vân sáng trùng nhau ta tính là một vân sáng)