Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(r_n=n^2r_0.\)
Bán kính quỹ đạo dừng N ứng với n = 4
\(r_N=r_4= 4^2r_0=16r_0.\)
Bán kính quỹ đạo dừng L ứng với n = 2
\(r_L=r_2= 2^2r_0=4r_0.\)
Như vậy khi electron chuyển từ quỹ đạo N về quỹ đạo L thì bán kĩnh quỹ đạo giảm
\(\Delta r= r_4-r_2= 16r_0-4r_0= 12r_0.\)

Đáp án D
Phương pháp: vận dụng biểu thức lực tính điện, lực hướng tâm, công thức bán kính quỹ đạo của Borh
Cách giải:
Lực tĩnh điện giữa e và hạt nhân đóng vai trò lực hướng tâm, nên ta có:
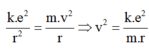
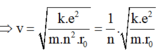
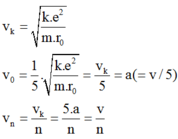
Chu kì chuyển động của hạt e trên quỹ đạo là:
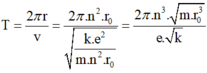
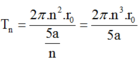
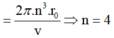
N = 4 là quỹ đạo dừng N

Đáp án B
Bán kính quỹ đạo dừng tại
![]()
Bán kính quỹ đạo dừng tại
![]()
Do đó bán kính quỹ đạo giảm là
![]()

Đáp án B
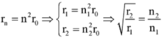 (1)
(1)
| n |
1 |
2 |
3 |
4 |
5 |
6…. |
| Tên |
K |
L |
M |
N |
O |
P…. |
Lực tác dụng giữa hạt nhân và electron trong nguyên tử hdro chính là lực hướng tâm, do đó:
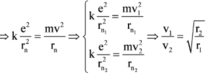 (2)
(2)
Từ (1) và (2)
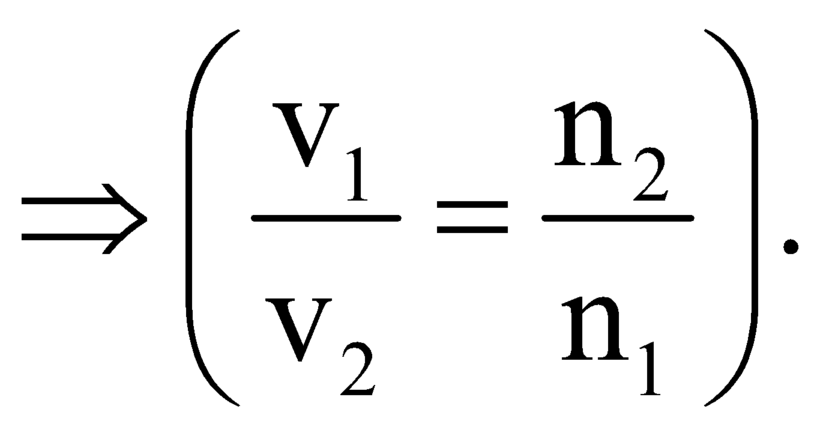
Áp dụng vào bài toán
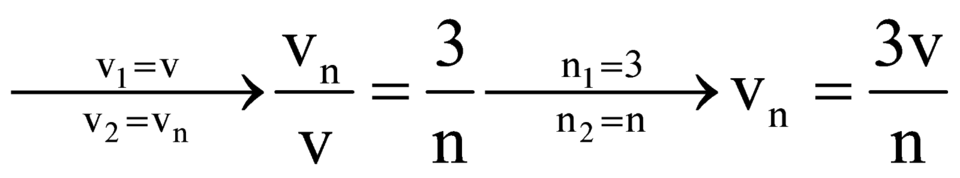
Chu kỳ
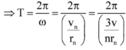
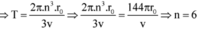

Đáp án A
Theo mẫu nguyên tử Bo
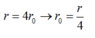
Từ quỹ đạo K lên N thì bán kính tăng
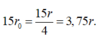
| Quỹ đạo |
K |
L |
M |
N |
| Bán kính |
ro |
4ro |
9ro |
16ro |

\(\frac{r}{r_0}=\frac{2,2.10^{-10}}{5,3.10^{-11}} \approx 4.\)
=> \(r = 4r_0 = 2^2 r_0.\) Tức là electron nhảy lên trạng thái dừng L (n = 2).

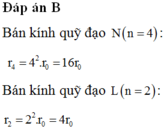
Khi electron chuyển từ quỹ đạo N về quỹ đạo L thì bán kính quỹ đạo giảm bớt
![]()



Chọn D.
Khi electron chuyển động trên quỹ đạo O thì bán kính r = n 2 r = 0 25 r 0 .