
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25

Hai câu c và d chỉ là BĐT \(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\), cách chứng minh \(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\) thế nào thì chứng minh c và d như vậy (biến đổi thành tổng của 3 bình phương các hiệu)
Với câu c thì \(x=ab;y=bc;z=ca\), câu d thì \(x=a^2b;y=...\)
Nhờ thầy viết cho em vài dòng câu d với ạ, câu d em chưa xử lý được thầy ạ?

1, VTCP \(\overrightarrow{AC}=\left(-2;2\right)\); A(4;3)
PTTS : \(\left\{{}\begin{matrix}x=4+2t\\y=3-2t\end{matrix}\right.\)( t là tham số )
VTPT ( -2;-2) ; A(4;3)
PTTQ : \(-2\left(x-4\right)-2\left(y-3\right)=0\Leftrightarrow-2x-2y+14=0\Leftrightarrow x+y-7=0\)
2, AB : \(VTCP\overrightarrow{AB}=\left(-10;-2\right)\)
Do delta vuông góc với AB nên VTCP AB là VTPT đt delta
delta \(-10\left(x-2\right)-2\left(y-5\right)=0\Leftrightarrow-10x-2y+30=0\Leftrightarrow5x+y-15=0\)
3, pt đường tròn có dạng \(\left(x+6\right)^2+\left(y-1\right)^2=R^2\)
do pt (C1) thuộc A nên \(\left(4+6\right)^2+\left(3-1\right)^2=R^2\Leftrightarrow104=R^2\)
=> \(\left(C1\right):\left(x+6\right)^2+\left(y-1\right)^2=104\)
4, tâm \(I\left(3;4\right)\)
\(R=\dfrac{AC}{2}=\dfrac{\sqrt{4+4}}{2}=\dfrac{\sqrt{8}}{2}\Rightarrow R^2=2\)
\(\left(C2\right):\left(x-3\right)^2+\left(y-4\right)^2=2\)

595:
a: \(\dfrac{cota\cdot cotb+1}{cota\cdot cotb-1}=\left(\dfrac{cosa}{sina}\cdot\dfrac{cosb}{sinb}+1\right):\left(\dfrac{cosa}{sina}\cdot\dfrac{cosb}{sinb}-1\right)\)
\(=\dfrac{cosa\cdot cosb+sina\cdot sinb}{sina\cdot sinb}:\dfrac{cosa\cdot cosb-sina\cdot sinb}{sina\cdot sinb}\)
\(=\dfrac{cos\left(a-b\right)}{cos\left(a+b\right)}\)
3: \(\dfrac{sin\left(a+b\right)sin\left(a-b\right)}{cos^2a\cdot cos^2b}=\dfrac{\left(sina\cdot cosb+sinb\cdot cosa\right)\left(sina\cdot cosb-sinb\cdot cosa\right)}{cos^2a\cdot cos^2b}\)
\(=\dfrac{sin^2a\cdot cos^2b-sin^2b\cdot cos^2a}{cos^2a\cdot cos^2b}\)
\(=\dfrac{sin^2a\cdot cos^2b-cos^2a\left(1-cos^2b\right)}{cos^2a\cdot\left(cos^2b\right)}\)
\(=\dfrac{sin^2a\cdot cos^2b+cos^2a\cdot cos^2b-cos^2a}{cos^2a\cdot cos^2b}=\dfrac{cos^2b-cos^2a}{cos^2a\cdot cos^2b}\)
tan^2a-tan^2b
=(sin^2a/cos^2a)-(sin^2b/cos^2b)
=(\(=\dfrac{\left(sina\cdot cosb\right)^2-\left(sinb\cdot cosa\right)^2}{cos^2a\cdot cos^2b}=\dfrac{\left(sina\cdot cosb-sinb\cdot cosa\right)\left(sina\cdot cosb+sinb\cdot cosa\right)}{cos^2a\cdot cos^2b}\)
=sin(a+b)sin(a-b)/cos^2a*cos^2b
4:
1-tan^2a*tan^2b
\(=1-\dfrac{sin^2a\cdot sin^2b}{cos^2a\cdot cos^2b}=\dfrac{cos^2a\cdot cos^2b-sin^2a\cdot sin^2b}{cos^2a\cdot cos^2b}\)
\(=\dfrac{\left(cosa\cdot cosb-sina\cdot sinb\right)\left(cosa\cdot cosb+sina\cdot sinb\right)}{cos^2a\cdot cos^2b}\)
\(=\dfrac{cos\left(a+b\right)\cdot cos\left(a-b\right)}{cos^2a\cdot cos^2b}\)

1: vecto AC=(-2;2)
=>VTCP là (-2;2); vtpt là (2;2)
2: vecto AB=(-10;-2)=(5;1)
=>VTPT của Δ là (5;1)
vtcp của Δ là (-1;5)
\(\overrightarrow{AC}=\left(-2;2\right)=2\left(-1;1\right)\) nên đường thẳng AC nhận \(\left(-1;1\right)\) là 1 vtcp và \(\left(1;1\right)\) là 1 vtpt
b.
\(\overrightarrow{BA}=\left(10;2\right)=2\left(5;1\right)\) ; mà \(\Delta\perp AB\) nên \(\Delta\) nhận (5;1) là 1 vtpt và \(\left(1;-5\right)\) là 1 vtcp

\(\dfrac{sin3x-cos3x}{sinx+cosx}=\dfrac{3sinx-4sin^3x-\left(4cos^3x-3cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sin^3x+cos^3x\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{sinx+cosx}\)
\(=3-4\left(1-sinx.cosx\right)=3-4+4sinx.cosx\)
\(=2sin2x-1\)

Thực hiện lần lượt BĐT cô-si 3 số cho từng bộ 3 vế trái, ví dụ:
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\ge3\sqrt[3]{\dfrac{1}{a^3b^3c^3}}=\dfrac{3}{abc}\)
Làm tương tự, sau đó cộng vế và quy đồng vế phải là sẽ được BĐT cần chứng minh


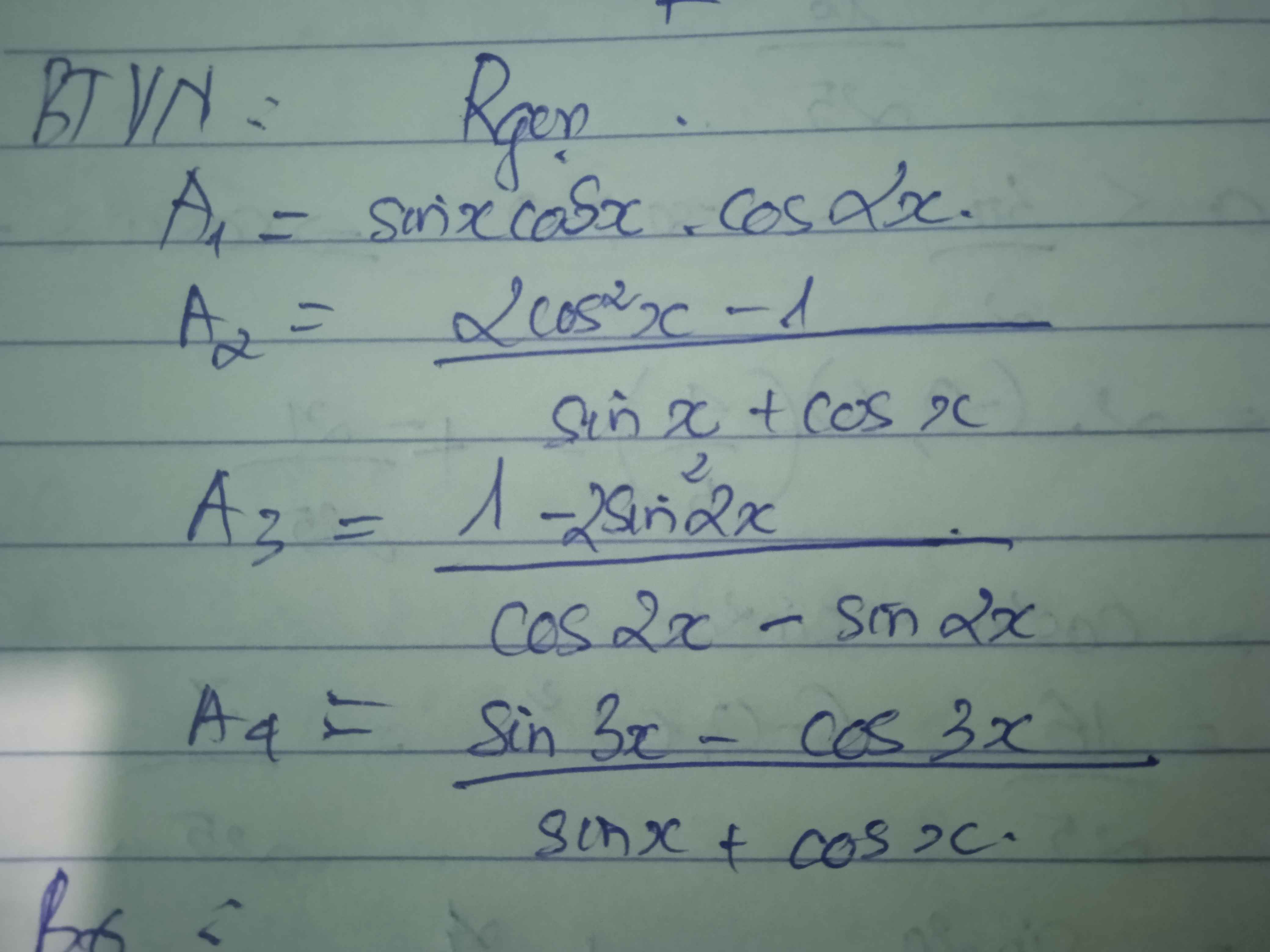






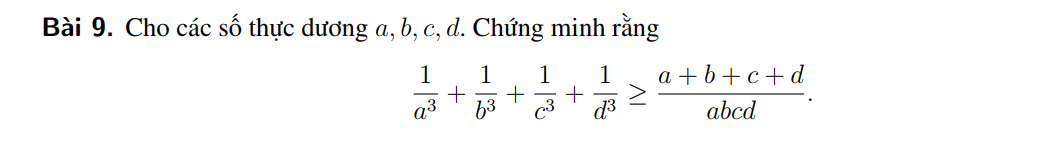
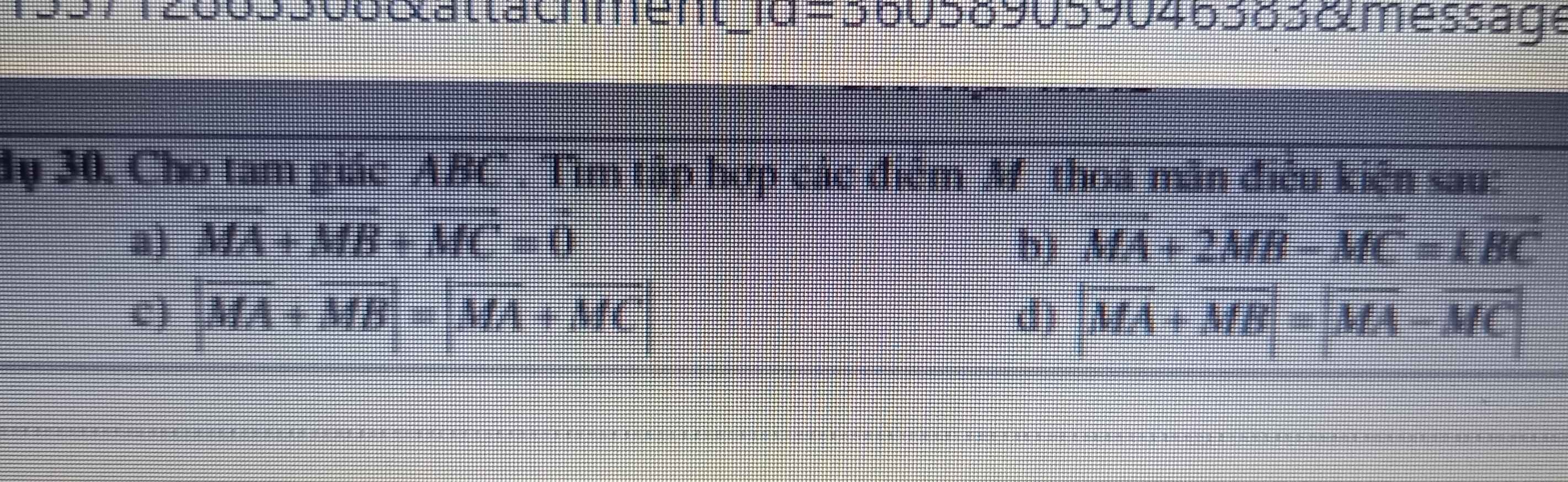
Không phải thầy cô nhma mình biết làm ,xin phép he:
1)
<=> \(\dfrac{cos\left(a-b\right)}{cos\left(a+b\right)}=\dfrac{cos\alpha.cosb+sina.sinb}{cosa.cosb-sina.sinb}\)
\(=\dfrac{\dfrac{cosa.cosb+sina.sinb}{sina.sinb}}{\dfrac{cosa.cosb-sina.sinb}{sina.sinb}}\)
( chia cả tử và mẫu cho sina.sinb).
\(=\dfrac{\dfrac{cosa}{sina}.\dfrac{cosb}{sinb}+1}{\dfrac{cosa}{sina}.\dfrac{cosb}{sinb}-1}\)
\(=\dfrac{cota.cotb+1}{cota.cotb-1}\)
trời tăng gp nhanh zữ zậy cj