Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D.
y' = 3 x 2 - 6(m - 1)x - 3(m + 1)
y' = 0 ⇔ x 2 - 2(m - 1)x - m - 1 = 0
Δ' = ( m - 1 ) 2 + m + 1 = m 2 - m + 2 ≥ 0
Tam thức m 2 - m + 2 luôn dương với mọi m ∈ R vì δ = 1 - 8 < 0 và a = 1 > 0 cho nên phương y' = 0 luôn có hai nghiệm phân biệt. Suy ra hàm số luôn có cực trị với mọi giá trị m ∈ R.

Đáp án: D.
y' = 3 x 2 - 6(m - 1)x - 3(m + 1)
y' = 0 ⇔ x 2 - 2(m - 1)x - m - 1 = 0
∆ ' = m - 1 2 + m + 1 = m 2 - m + 2 ≥ 0
Tam thức m 2 - m + 2 luôn dương với mọi m ∈ R vì δ = 1 - 8 < 0 và a = 1 > 0 cho nên phương y' = 0 luôn có hai nghiệm phân biệt. Suy ra hàm số luôn có cực trị với mọi giá trị m ∈ R.

Chọn D
Hàm số y = log ( x 2 - 4 x - m + 1 ) có tập xác định là ℝ khi và chỉ khi
![]()
![]()

Chọn D
Hàm số xác định với mọi ![]() thì
thì  luôn đúng với mọi
luôn đúng với mọi ![]()
+) Ta có: ![]()
![]()
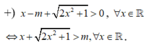
Xét hàm số ![]()
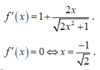
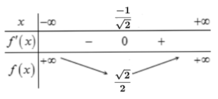
Từ bảng biến thiên ta thấy để 
Kết hợp điều kiện
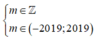
![]()
Kết luận: có 2019 giá trị của m thỏa mãn bài toán.

Đáp án: B.
Hàm số đã cho có cực trị khi và chỉ khi
y' = 3 x 2 - 6(m - 1)x - 3(m + 3) = 0 có 2 nghiệm phân biệt
⇔ ∆ ' = m - 1 2 + (m + 3) = m 2 - m + 4 > 0
Ta thấy tam thức ∆ ' = m 2 - m + 4 luôn dương với mọi m vì
δ = 1 - 16 = -15 < 0, a = 1 > 0
Vậy hàm số đã cho luôn có cực trị mới mọi m ∈ R
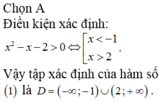

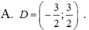
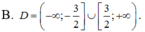
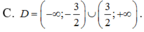
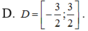
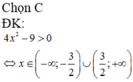

Hàm số log0,5(x + 1) xác định khi x + 1 > 0 ⇔ x > -1.
Chọn A.