
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Không thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác vì đường trung tuyến qua một đỉnh của tam giác và trung điểm một cạnh trong tam giác nên đường trung tuyến phải nằm giữa hai cạnh của một tam giác tức nằm ở bên trong của một tam giác nên ba đường trung tuyến cắt nhau chỉ có thể nằm bên trong của tam giác.

a) - Trọng tâm của một tam giác có tính chất như sau:
"Trọng tâm cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó."
- Các cách xác định trọng tâm:
+ Cách 1: Vẽ hai đường trung tuyến ứng với hai cạnh tùy ý, rồi xác định giao điểm của hai đường trung tuyến đó.
+ Cách 2: Vẽ một đường trung tuyến của tam giác. Chia độ dài đường trung tuyến thành ba phần bằng nhau rồi xác định một điểm cách đỉnh hai phần bằng nhau.
b) Không thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác vì đường trung tuyến qua một đỉnh của tam giác và trung điểm một cạnh trong tam giác nên đường trung tuyến phải nằm giữa hai cạnh của một tam giác tức nằm ở bên trong của một tam giác nên ba đường trung tuyến cắt nhau chỉ có thể nằm bên trong của tam giác.
Trả lời
a) - Trọng tâm của một tam giác có tính chất như sau:
"Trọng tâm cách đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó."
- Các cách xác định trọng tâm:
+ Cách 1: Vẽ hai đường trung tuyến ứng với hai cạnh tùy ý, rồi xác định giao điểm của hai đường trung tuyến đó.
+ Cách 2: Vẽ một đường trung tuyến của tam giác. Chia độ dài đường trung tuyến thành ba phần bằng nhau rồi xác định một điểm cách đỉnh hai phần bằng nhau.
b) Không thể vẽ được một tam giác có trọng tâm ở bên ngoài tam giác vì đường trung tuyến qua một đỉnh của tam giác và trung điểm một cạnh trong tam giác nên đường trung tuyến phải nằm giữa hai cạnh của một tam giác tức nằm ở bên trong của một tam giác nên ba đường trung tuyến cắt nhau chỉ có thể nằm bên trong của tam giác.

a, Trọng tâm của tam giác cách đỉnh 2/3 đường trung tuyến đi qua đỉnh ấy
Cánh xác định trọng tâm: vẽ 2 đường trung tuyến của tam giác, 2 đường đó cắt nhau tại điểm nào thì đó là trọng tâm của tam giác
b, Bạn Nam nói sai. Vì 3 đường trung tuyến của tam giác luôn ở trong tam giác nên giao điểm của chúng hay trọng tâm của tam giác luôn ở trong tam giác

a) Tính chất trong SGK . Xác định thì đầy cách.
Cách 1 : Chứng minh là giao điểm 2 đường trung tuyến
Cách 2 : Gỉa sử AM là trung tuyến ,G thuộc AM Chứng minh \(GM=\frac{1}{3}AM\)thì là trọng tâm Hoặc tùy
Cách khác là cách nâng cao
Câu 7 :
Tam giác cân, tam giác đều
Câu 8:
Tam giác đều
b) Trung tuyến xuất phát từ đỉnh và đi qua trung điểm của cạnh đối diện.
3 trung tuyến cùng cắt nhau tại 1 điểm là trọng tâm
Vì vậy ko thể nào có trọng tâm nằm ngoài tam giác ( vìTrung tuyến xuất phát từ đỉnh và đi qua trung điểm của cạnh đối diện nó nằm ngoài thì gọi gì là trung tuyến nữa )
suy ra Nam sai

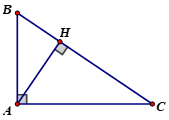
+ Xét ΔABC vuông tại A
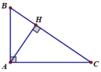
AB ⏊AC ⇒ AB là đường cao ứng với cạnh AC và AC là đường cao ứng với cạnh AB
hay AB, AC là hai đường cao của tam giác ABC.
Mà AB cắt AC tại A
⇒ A là trực tâm của tam giác vuông ABC.
Vậy: trực tâm của tam giác vuông trùng với đỉnh góc vuông
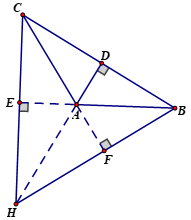
+ Xét ΔABC tù có góc A tù, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
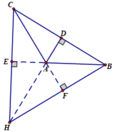
+ Giả sử E nằm giữa A và B, khi đó
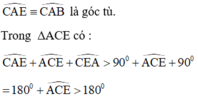
Vậy E nằm ngoài A và B
⇒ tia CE nằm ngoài tia CA và tia CB ⇒ tia CE nằm bên ngoài ΔABC.
+ Tương tự ta có tia BF nằm bên ngoài ΔABC.
+ Trực tâm H là giao của BF và CE ⇒ H nằm bên ngoài ΔABC.
Vậy : trực tâm của tam giác tù nằm ở bên ngoài tam giác.

+ Xét ΔABC vuông tại A
AB ⏊AC ⇒ AB là đường cao ứng với cạnh AC và AC là đường cao ứng với cạnh AB
hay AB, AC là hai đường cao của tam giác ABC.
Mà AB cắt AC tại A
⇒ A là trực tâm của tam giác vuông ABC.
Vậy: trực tâm của tam giác vuông trùng với đỉnh góc vuông
+ Xét ΔABC tù có góc A tù, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
+ Giả sử E nằm giữa A và B, khi đó
\(CAE\equiv CAB\)(góc tù)
tam giac ACE có: cae+ace+cea >90độ+ace+90độ
=180 độ+ace>180 độ
Vậy E nằm ngoài A và B
⇒ tia CE nằm ngoài tia CA và tia CB ⇒ tia CE nằm bên ngoài ΔABC.
+ Tương tự ta có tia BF nằm bên ngoài ΔABC.
+ Trực tâm H là giao của BF và CE ⇒ H nằm bên ngoài ΔABC.
Vậy : trực tâm của tam giác tù nằm ở bên ngoài tam giác.
Kiến thức áp dụng
+ Ba đường cao trong tam giác đồng quy tại một điểm. Do đó khi xác định trực tâm ta chỉ cần xác định giao của hai đường cao.
+ Định lý tổng ba góc trong một tam giác : Trong một tam giác, tổng ba góc bằng 180độ
+ Xét ΔABC vuông tại A
AB ⏊AC ⇒ AB là đường cao ứng với cạnh AC và AC là đường cao ứng với cạnh AB
hay AB, AC là hai đường cao của tam giác ABC.
Mà AB cắt AC tại A
⇒ A là trực tâm của tam giác vuông ABC.
Vậy: trực tâm của tam giác vuông trùng với đỉnh góc vuông
+ Xét ΔABC tù có góc A tù, các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
+ Giả sử E nằm giữa A và B, khi đó
Vậy E nằm ngoài A và B
⇒ tia CE nằm ngoài tia CA và tia CB ⇒ tia CE nằm bên ngoài ΔABC.
+ Tương tự ta có tia BF nằm bên ngoài ΔABC.
+ Trực tâm H là giao của BF và CE ⇒ H nằm bên ngoài ΔABC.
Vậy : trực tâm của tam giác tù nằm ở bên ngoài tam giác.

Trực tâm của tam giác vuông trùng với đỉnh góc vuông là vì mỗi cạnh góc vuông của tam giác chính là đường cao cua tam giác nên 2 cạnh góc vuông và đường cao ứng với cạnh huyền trong tam giác vuông cắt nhau tại đỉnh góc vuông.
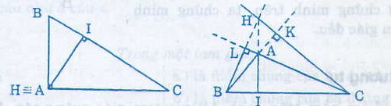
+ Nếu tam giác ABC có góc A tù => BC là cạnh lớn nhất
=> BC > BA
Kẻ đường cao BL thì LA; LC là hai hình chiếu của BA, BC => LA < LC
=> A nằm giữa L và C tức đường cao BL nằm ngoài tam giác ABC
Tương tự đường cao CK nằm ngoài tam giác ABC
Nên điểm cắt nhau của ba đường cao nằm ngoài tam giác
Trực tâm của tam giác vuông trùng với đỉnh góc vuông vì tam giác vuông có 2 đường cao cắt nhau tại đỉnh của tam giác vuông nên đường cao thứ 3 cũng đồng quy tại đỉnh của tam giác vuông.
Trực tâm của tam giác tù nằm ngòai tam giác vì tam giác tù có 2 đường cao kẻ từ 2 góc nhọn nằm ngoài tam giác và cắt nhau tại đỉem ngoài tam giác do đó đừng cao còn lại tức kẻ từ góc tù sẽ đồng quy với 2 đường cao kia tại giao điểm nằm ngoài tam giác.
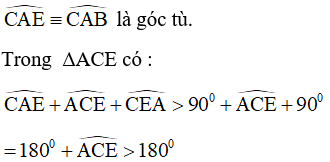
Vì tất cả trung tuyến đều nằm trong tam giác => trọng tâm chắc chán phải nằm trong tam giác