K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
1
28 tháng 5 2022
Câu 1: Hai góc đối đỉnh bằng nhau vì chúng cùng kề bù với một góc
Câu 2: Hai đường thẳng phân biệt vuông góc với nhau khi chúng cắt nhau và trong các góc tạo thành, có một góc bằng 90 độ
Câu 3: Hai đường thẳng phân biệt song song với nhau khi chúng không có điểm chung
NN
1
BD
19 tháng 10 2016
Theo mình biết tổng 3 góc trong một tam giác = 180 độ là một tiên đề (tương đương với tiên đề 5 của Ơclit) đến bây giờ có thể khẳng định rằng ko thể chứng minh được. Việc phủ định lại tiên đề trên mở ra một chân trời mới cho toán học, đồng thời đã có thành tựu vô cùng rực rỡ, điển hình là trong lĩnh vực hàng không vũ trụ và 1 lí thuyết vĩ đại "Thuyết tương đối".
Phải công nhận tổng 3 góc 1 \(\exists\) =180 độ mới có những kết quả về đường thẳng song song.
nhé !
NH
3
22 tháng 6 2018
Ta có :
\(\left(x-1\right)^x=1\)
Trường hợp x chẵn :
\(\Leftrightarrow\)\(\orbr{\begin{cases}x-1=1\\x-1=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1+1=2\\x=-1+1=0\end{cases}}}\)
Trường hợp x lẻ :
\(\left(x-1\right)^x=1^x\)
\(\Leftrightarrow\)\(x-1=1\)
\(\Leftrightarrow\)\(x=1+1\)
\(\Leftrightarrow\)\(x=2\)
Vậy \(x=0\) hoặc \(x=2\)
* Giải thích :
\(x-1=\pm1\)
Vì nếu x là số chẵn thì x sẽ có dạng \(2n\) \(\left(n\inℕ\right)\)
Khi đó \(VT=\left(x-1\right)^x=\left(x-1\right)^{2n}=\left[\left(x-1\right)^n\right]^2\)
\(VP=1=1^2\)
\(\Rightarrow\)\(x-1=\pm1\)
Chúc bạn học tốt ~
DC
3
31 tháng 7 2018
\(\left(\frac{1}{a}+\frac{1}{b}\right).\left(a+b\right)\)
\(=1+\frac{a}{b}+1+\frac{b}{a}\)
\(=2+\frac{a}{b}+\frac{b}{a}\)
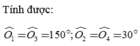
Có
\(2^n\cdot5=(2^{n-1}\cdot2)\cdot5=2^{n-1}\cdot2\cdot5=2^{n-1}\cdot10\\ \Rightarrow2^n\cdot5=2^{n-1}\cdot10\)