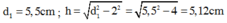Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chọn đáp án D
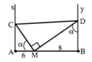
Theo đề bài thì ta thấy ABCD sẽ được lập thành 1 hình thang cân, Đáy lớn là AB, đáy nhỏ CD. Chiều cao H là đáp án cần tìm.Để cho trên đoạn CD chỉ có 3 điểm dao động cực đại thì đồng nghĩa chỉ có 2 hypebol giao CD (1 còn lại là vân trung tâm) vậy thì CD giao các hepybol K=1
Lúc này , để các điểm đó là cực đại thì
D
2
-
D
1
=
K
λ
, ta sẽ xác định tọa độ C và D rồi lồng vào bất đẳng thức sau
B
D
-
A
D
≤
k
λ
≤
B
C
-
A
C
các độ dài của đoạn BC, AC hay các đoạn thành phần của AB các bạn vẽ hình ra để thấy cho rõ nhé !
Ta thấy H chỉ nhỏ nhất khi CB-AC nhỏ nhất
⇔
B
C
-
A
C
=
1
.
5
(
1
)
ta lại có :
B
C
2
=
H
2
+
6
2
(
2
)
và
A
C
2
=
H
2
+
2
2
(
3
)
Áp dụng hằng đẳng thức :
A
2
-
B
2
để lấy (2) - (3) ,tiếp đến lấy phương trình (1) thế vào phương trình vừa tính ta được
(
A
C
+
B
C
)
=
32
1
.
5
Giải hệ (1) và (4) ta tìm được BC và AC , từ đó tìm được H = 9.7


Bước sóng: \(\lambda=\dfrac{v}{f}=\dfrac{30}{20}=1,5cm\)
Trên CD có 5 cực đại và khoảng cách từ CD đến AB là lớn nhất, suy ra mép C, D thuộc cực đại thứ 2.
\(\Rightarrow CB-CA =2\lambda=3cm\)
\(HO=CI=6/2=3cm\)
\(AH=7-3=4(cm)\)
\(BH=7+3=10(cm)\)
Ta có: \(CB^2=HB^2+CH^2=10^2+CH^2\) (1)
\(CA^2=AH^2+CH^2=4^2+CH^2\) (2)
Lấy (2) - (1) vế với vế \(\Rightarrow CB^2-CA^2=10^2-4^2=84\)
\(\Rightarrow (CB-CA)(CB+CA)=84\)
\(\Rightarrow CB+CA = 84:3 = 28\)
Có: \(CB-CA=3\)
\(\Rightarrow CB = 15,5(cm)\)
\(\Rightarrow CH=\sqrt{CB^2-HB^2}=\sqrt{15,5^2-10^2}=11,84cm\)
Chọn A.

Đáp án D
∆
A
M
C
đồng dạng với
∆
B
D
M
suy ra 

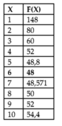
* Bấm ![]() và nhập hàm
và nhập hàm
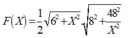
Chọn  , thu được bảng bên phải
, thu được bảng bên phải
Dễ thấy ![]()
v Điều kiện vân cực đại

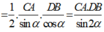
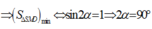

Bình luận: Thay vì đạo hàm hay dùng bất đẳng thứcCô Si thì các em học sinh có thể dùng máy tính cầm tay để tìm giá trị nhỏ nhất rất nhanh chóng.
*Cách dùng bất đẳng thức Côsi
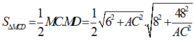 . (Đặt AC=x →biến số).
. (Đặt AC=x →biến số).
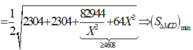
![]()
vậy với cách làm này thì các em cũng có thể tìm được giá trị của AC=6 để cho diện tích tam giác MCD nhỏ nhất.

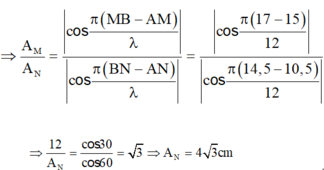
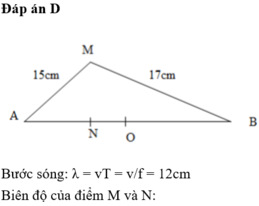
Đáp án D
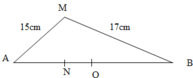
Bước sóng: λ = vT = v/f = 12cm
Biên độ của điểm M và N:
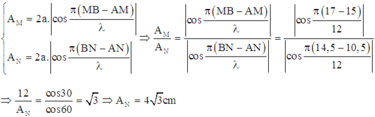

Bước sóng \(\lambda=\frac{v}{f}=2cm\)
Số điểm dao động với biên độ cực tiểu ứng với số giá trị của k: \(-\frac{AB}{\lambda}-0,5\le k\le\frac{AB}{\lambda}-0,5\)
\(\Leftrightarrow-5,5\le k\le4,5\)
Suy ra có 10 giá trị của k, tức là có 10 điểm dao động với biên độ cực tiểu trên AB
Đáp án C


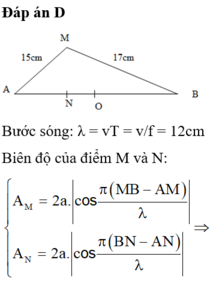
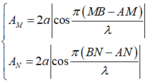
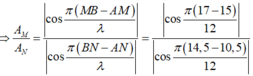

Đáp án D
Bước sóng .
.
Khoảng cách lớn nhất từ CD đến AB mà trên CD chỉ có 3 điểm dao động với biên độ cực đại khi tại C và D thuộc các vân cực đại bậc 1.
Tại C: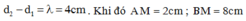
Suy ra