Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Trên dây có sóng dừng với 5 bó sóng → λ = 2 l n = 2.15 5 = 6 cm.
+ Biên độ dao động của điểm cách nút một đoạn d được xác định bằng biểu thức:
A = A b sin 2 π d λ → A M = 1. sin 2 π .4 6 = 3 2 A M = 1. sin 2 π .8 6 = 3 2 cm.
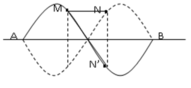
+ M và N nằm trên hai bó sóng liên tiếp nhau → M N m i n khi M, N cùng đi qua vị trí cân bằng; M N m a x khi M, N ở vị trí biên.
→ M N m a x M N min = 3 2 + 3 2 3 = 1 , 2
+ Trên dây có 2 bụng sóng nên: λ = 2 l k = 2.24 2 = 24 cm
+ Khi dây duỗi thẳng thì M, N chia dây làm 3 đoạn bằng nhau nên: AM = MN = NB = 8 cm.
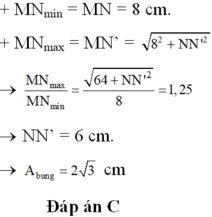
+ MNmin = MN = 8 cm.
+ MNmax = MN’ = 8 2 + N N ' 2
® M N max M N min = 64 + N N ' 2 8 = 1 , 25 ® NN’ = 6 cm.
® A b ung = 2 3 cm
ü Đáp án C
Đáp án C.
Trên dây có sóng dừng với hai bụng sóng nên
.
M, N thuộc hai bó sóng liên tiếp nên ngược pha nhau.
Khoảng cách MN nhỏ nhất khi M, N ở vị trí cân bằng hay
.
Gọi trung điểm MN là O (khi đó chính là một nút) thì OM = 4cm = λ/6.
Vậy biên độ dao động của M và N là:
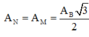(vì M và N đối xứng nhau qua nút biên độ dao động bằng nhau).
Khoảng cách M, B lớn nhất là
khi M, N nằm ở biên.
Mặt khác
.
Đáp án C
+ A, B là nút sóng, trên dây AB có bụng sóng ⇒ λ = l = 24 c m
+ M, N là hai điểm trên dây chia thành 3 đoạn bằng nhau khi dây duỗi thẳng → M, N cách nút sóng gần đó nhất đoạn λ 6 = 4 c m
⇒ A M = A N = A b sin 2 π . λ 6 λ = 3 c m
+ M, N thuộc hai bó liên tiếp nhau nên dao động ngược pha với nhau.
+ Khoảng cách MN nhỏ nhất khi sợi dây duỗi thẳng M N min = A B 3 = 8 c m
+ Khoảng cách MN lớn nhất khi M, N cùng đến biên:
M N max = A B 3 2 + A M + A M 2 = 10 c m
+ Vậy δ = M N max M N min = 10 8 = 1 , 25
Đáp án C
+ Khi xuất hiện sóng dừng, trên dây có hai bụng sóng → sóng dừng trên dây với hai bó sóng → λ = 24cm → M và N lần lượt cách nút gần nhất một đoạn λ/6 = 4 cm.
A N = A M = A b 3 2 = 2 3 3 2 = 3 cm .
+ M và N thuộc hai bó sóng liên tiếp nên dao động ngược pha nhau → MN lớn nhất khi M và N cùng đến biên, MN nhỏ nhất khi M và N cùng đến biên, MN nhỏ nhất khi M, N cùng đi qua vị trí cân bằng.
→ σ = MN 2 + ( 2 A N ) 2 MN 2 = 8 2 + 6 2 8 2 = 1 , 25 .
Đáp án D
M và N nằm trên hai bó sóng liên tiếp sẽ dao động ngược pha nhau
+ Khoảng cách giữa M và N nhỏ nhất khi M và N cùng đi qua vị trí cân bằng theo hai chiều ngược nhau d min = λ 3 = 8 cm
+ Khoảng cách giữa M và N lớn nhất khi M và N đang ở vị trí biên d m a x = 1 , 25 d min = 1 , 25.8 = 10 cm
Từ hình vẽ ta có d m a x = 2 A M 2 + d min 2 → A M = 3 cm
+ M cách bụng gần nhất một đoạn λ 6 → A M = 3 2 A = 2 3 cm
Đáp án A
+ Khi xảy ra sóng dừng trên dây có 20 bụng sóng
+ Biên độ dao động của các phần tử dây cách nút A một đoạn d được xác định bằng biểu thức:
với 
là biên độ của điểm bụng
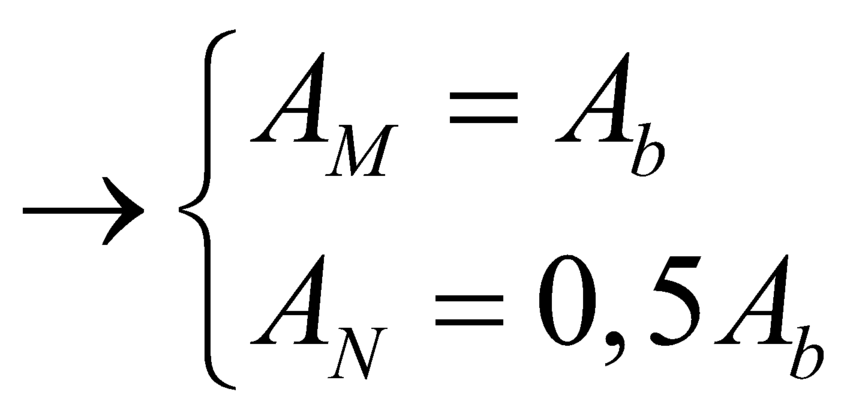
+ Theo giả thuyết của bài toán
b.
Ta có $\lambda =24cm $
Bạn vẽ hình ra .
Đoạn AB =24cm sau đó vẽ 2 bụng sóng.
Lấy M N nằm giữa sao cho MN= AB/3 = 8 cm.
Khoảng cách MN lớn nhất khi chúng nằm trên bụng và nhỏ nhất khi duỗi thẳng.
Ta có $\dfrac{MN_{lớn}}{MN_{nhỏ}} =1.25 \rightarrow MN_{lớn}=10 \rightarrow $biên độ của M và N là 3cm.
Khoảng cách từ M đến nút bằng 4cm =$\dfrac{\lambda}{6} \rightarrow A_{bụng} =2\sqrt{3}$