PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
20 tháng 1 2021
a) Xét tam giác AMB có :
MO = OA = OB ( =bk )
\(\Rightarrow MO=\frac{1}{2}AB\)
=> Tam giác AHB vuông tại M
=> EM là đường cao của tam giác ANE
- Xét tam giác ACB có : OC = OB = OA ( =bk )
\(\Rightarrow OC=\frac{1}{2}AB\Rightarrow\Delta ACB\)vuông tại C
=> NC là đường cao của tam giác ANE
=> B là giao điểm 3 đường cao của tam giác ANE
=> AB là đường cao của tam giác ANE
Vậy : \(NE\perp AB\left(đpcm\right)\)
b) Xét 2tam giác : MAF và MNE
Có : MA = MN (gt)
MF = ME ( gt )
^AMF = ^NME ( đối đỉnh )
do đó : \(\Delta MAF=\Delta NME\left(c-g-c\right)\)
=> ^AFM = ^NEM
Mà 2 góc ^AFM và ^NEM có vị trí so le
=> AF // NE
Mà : \(NE\perp AB\)( c/m câu a ) => \(AF\perp AB\)tại A
Vậy : FA là tiếp tuyến đường tròn (O) ( đpcm )
c) Ta có : ^AMB = 90^o => \(FB\perp AN\)
MA = MB
=> FB là đường trung trực của AN
=> BN = BA ; FN = FA
- Xét 2 tam giác : ABF và NBF có : BN = BA ; FN = FA
FB chung
\(\Rightarrow\Delta ABF=\Delta NBF\left(c-c-c\right)\)
=> ^BNF = ^BAF = 90^o
\(\Rightarrow BN\perp FN\)tại B mà BN = BA
Vậy : FN là tiếp tuyến của đường tròn ( B ; BA ) ( đpcm )
CM
27 tháng 3 2018
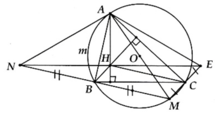
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3
Đáp án A
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn