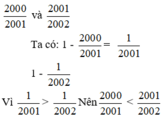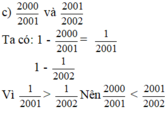Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 20012001 + 1999 x 20012001
A = 20012001 x (1+1999)
A = 20012001 x 2000
B = 20012002 x 2001 - 20012001
B = (20012001+1) x 2001 - 20012001
B = 20012001 x 2001 + 20012001 - 20012001
B = 20012001 x 2001
Vì 20012001 x 2000 < 20012001 x 2001 nên A < B
A = 20012001 x 2000
b = 20012001 x 2001
vì 20012001 x 2000 < 20012001 x 2001 nên A < B k cho tui nha

a. Ta tính trước số bị chia: 1 + 4 + 7 + …… + 100
Dãy số gồm có: (100 – 1) : 3 + 1 = 34 (số hạng)
Ta thấy: 1 + 100 = 4 + 97 = 101 = …..
Do đó số bị chia là: 101 x 34 : 2 = 1717
Ta có: 1717 : a = 17
a = 1717 : 17
a = 101
vậy a = 101.
b.
x - 1 2 × 5 3 = 7 4 - 1 2 x - 1 2 × 5 3 = 5 4 x - 1 2 = 5 4 : 5 3 x - 1 2 = 3 4 x = 3 4 + 1 2 x = 5 4
c. 2000 2001 v à 2001 2002
Ta có: 1 - 2000 2001 = 1 2001
1 - 2001 2002 = 1 2002
Vì 1 2001 > 1 2002 nên 2000 2001 < 2001 2002

Ta có:
B=\(\frac{2000+2001}{2001+2002}=\frac{2000}{2001+2002}+\frac{2001}{2001+2002}\)
Do \(\frac{2000}{2001}>\frac{2000}{2001+2002};\frac{2001}{2002}>\frac{2001}{2001+2002}\)
\(\Rightarrow\frac{2000}{2001}+\frac{2001}{2002}>\frac{2000}{2001+2002}+\frac{2001}{2001+2002}\)
\(\Rightarrow A>B\)
Vậy \(A>B\)
Ta có:$B=\frac{2000}{2001+2002}+\frac{2001}{2001-2002}$B=20002001+2002 +20012001−2002
Vì:$\frac{2000}{2001}>\frac{2000}{2001+2002}$20002001 >20002001+2002
$\frac{2001}{2002}>\frac{2001}{2001+2002}$20012002 >20012001+2002
$\Rightarrow\left(\frac{2000}{2001}+\frac{2001}{2002}\right)>\left(\frac{2000}{2001-2002}-\frac{2001}{2001+2001}\right)$⇒(20002001 +20012002 )>(20002001−2002 −20012001+2001 )
$\Rightarrow A>B$⇒A>B

a = 2002 . 2002 = 2002 . (2000 + 2) = 2002 . 2000 + 2002 . 2
b = 2000 . 2004 = 2000 . (2002 + 2) = 2000 . 2002 + 2000 . 2
Do: 2002 . 2 > 2000 . 2 => 2002 . 2000 + 2002 . 2 > 2000 . 2002 + 2000 . 2
=> 2002 . 2002 > 2000 . 2004 => a > b

Xét vế 1999×2001-1/1998×1999×2000
=1999×(1998+3)-1/1998×1999×2000
=1999×1998+1999×3-1/1998×1999×2000
=1999×1998+5996/1998×1999×2000
Sai đề rồi bạn ơi