HD
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
ML
5 tháng 2 2016
Gọi 3 máy là a,b,c. Ta có:
a+b = 1 giờ 20 phút = 80 (phút)
b+c = 1 giờ 30 phút = 90 (phút)
a+c = 2 giờ 24 phút = 144 (phút)
mà a+b+b+c+a+c = 80+90+144 = 314 ( phút)
hay 2(a+b+c) = 314 => a+b+c = 314/2 = 157
- c = (a+b+c) - (a+b) = 157 - 80 = 77 (phút)
- a = (a+b+c) - (b+c) = 157 - 90 = 67 (phút)
- b = (a+b+c) - (a+c) = 157 - 144 = 13 (phút)
VM
11 tháng 12 2019
\(12^8.9^{12}\) và \(18^{18}.\)
Ta có:
\(12^8.9^{12}\)
\(=\left(2^2.3\right)^8.\left(3^2\right)^{12}\)
\(=2^{16}.3^8.3^{24}\)
\(=2^{16}.3^{32}\)
\(=2^{16}.\left(3^2\right)^{16}\)
\(=2^{16}.9^{16}\)
\(=\left(2.9\right)^{16}\)
\(=18^{16}.\)
Vì \(18^{16}< 18^{18}.\)
\(\Rightarrow12^8.9^{12}< 18^{18}.\)
Chúc bạn học tốt!
TL
3
5 tháng 11 2016
x+y =9,8 và x=-3,1
-> y= 9,8 - (-3,1) =9,8+3,1
-> 9,8 + 3,1 >0
-> y >0
-> x < 0<y
A
22 tháng 6 2019
1.
Ta có 3223 > 3222 = (32)111 = 9111. (1)
2332 < 2333 = (23)111 = 8111. (2)
Từ (1) và (2) suy ra: 2332 < 8111 < 9111 < 3223.
Vậy 2332 < 3223
2.
Cách 1: 92000 = (32)2000 = 34000
Cách 2: 34000 = (34)1000 = 811000. (1)
92000 = (92)1000 = 811000. (2)
Từ (1) và (2) suy ra 34000 = 92000 .
3.
Đặt A = 22009 + 22008 + ... + 21 + 20
Ta có 2A = 22010 + 22009 + ... + 22 + 21.
Suy ra 2A - A = 22010 - 20 = 22010 - 1.
Do đó M = 22010 - A = 22010 - (22010 - 1) = 1.
22 tháng 6 2019
trả lời;
1)2332 và 3223
2332 <2333 mà 2333=(23)111=8111
3223 >3222 mà 3222=(32)111=9111
từ (1 và 2),suy ra:8111<9111 hay 2332<3223
HH
14 tháng 6 2018
Giải:
\(C=\left(1-\dfrac{2}{2.3}\right)\left(1-\dfrac{2}{3.4}\right)\left(1-\dfrac{2}{4.5}\right)...\left(1-\dfrac{2}{n\left(n+1\right)}\right)\)
Đk: \(n\ne0;n\ne-1\)
\(C=\left(1-\dfrac{2}{2.3}\right)\left(1-\dfrac{2}{3.4}\right)\left(1-\dfrac{2}{4.5}\right)...\left(1-\dfrac{2}{n\left(n+1\right)}\right)\)
\(\Leftrightarrow C=\left(\dfrac{2.3-2}{2.3}\right)\left(\dfrac{3.4-2}{3.4}\right)\left(\dfrac{4.5-2}{4.5}\right)...\left(\dfrac{n\left(n-1\right)-2}{n\left(n+1\right)}\right)\)
\(\Leftrightarrow C=\dfrac{4}{2.3}.\dfrac{10}{3.4}.\dfrac{18}{4.5}...\left(\dfrac{n\left(n-1\right)-2}{n\left(n+1\right)}\right)\)
\(\Leftrightarrow C=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\left(\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\right)\)
\(\Leftrightarrow C=\dfrac{1.4.2.5.3.6...\left(n-1\right)\left(n+2\right)}{2.3.3.4.4.5.n\left(n+1\right)}\)
\(\Leftrightarrow C=\dfrac{\left[1.2.3...\left(n-1\right)\right]\left[4.5.6\left(n+2\right)\right]}{\left(2.3.4...n\right)\left[3.4.5....\left(n+1\right)\right]}\)
\(\Leftrightarrow C=\dfrac{n+2}{3n}\)
Vì \(\dfrac{n+2}{3n}< \dfrac{2n+2}{3n}\)
\(\Leftrightarrow C< \dfrac{2n+2}{3n}\)
Vậy ...
HH
14 tháng 6 2018
Giải:
\(C=\left(1-\dfrac{2}{2.3}\right)\left(1-\dfrac{2}{3.4}\right)\left(1-\dfrac{2}{4.5}\right)...\left(1-\dfrac{2}{n\left(n+1\right)}\right)\)
Đk: \(n\ne0;n\ne-1\)
\(C=\left(1-\dfrac{2}{2.3}\right)\left(1-\dfrac{2}{3.4}\right)\left(1-\dfrac{2}{4.5}\right)...\left(1-\dfrac{2}{n\left(n+1\right)}\right)\)
\(\Leftrightarrow C=\left(\dfrac{2.3-2}{2.3}\right)\left(\dfrac{3.4-2}{3.4}\right)\left(\dfrac{4.5-2}{4.5}\right)...\left(\dfrac{n\left(n-1\right)-2}{n\left(n+1\right)}\right)\)
\(\Leftrightarrow C=\dfrac{4}{2.3}.\dfrac{10}{3.4}.\dfrac{18}{4.5}...\left(\dfrac{n\left(n-1\right)-2}{n\left(n+1\right)}\right)\)
\(\Leftrightarrow C=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\left(\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\right)\)
\(\Leftrightarrow C=\dfrac{1.4.2.5.3.6...\left(n-1\right)\left(n+2\right)}{2.3.3.4.4.5.n\left(n+1\right)}\)
\(\Leftrightarrow C=\dfrac{\left[1.2.3...\left(n-1\right)\right]\left[4.5.6\left(n+2\right)\right]}{\left(2.3.4...n\right)\left[3.4.5....\left(n+1\right)\right]}\)
\(\Leftrightarrow C=\dfrac{n+2}{3n}\)
Vì \(\dfrac{n+2}{3n}< \dfrac{2n+2}{3n}\)
\(\Leftrightarrow C< \dfrac{2n+2}{3n}\)
Vậy ...
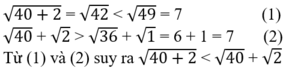
Ta có: \(\sqrt{2}>1\)
\(\Rightarrow1+\sqrt{2}>1+1\)
\(\Rightarrow1+\sqrt{2}>2\)
Ta có:\(\sqrt{2}>\sqrt{1}\)
\(\Leftrightarrow1+\sqrt{2}>1+\sqrt{1}=2\)