Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a)=1/3-[(-5/4)-5/8]
=1/3-(-15/8)=53/24
b)=5/9:(-3/22)+5/9:(-3/5)
=5/9*22/-3+5/9*5/-3=-110/27+-25/27=5
2
a)Ta có 339<340=920<1120<1121
nên 339<1121
b)Ta có /3,4-x/ lớn hơn hoặc bằng 0 Với mọi x thuộc R
=> -/3,4-x/ bé hơn hoặc bằng 0 Với mọi x thuộc R
=> 0,5-/3,4-x/ bé hơn hoặc bằng 0,5 Với mọi x thuộc R
Dấu = xảy ra khi 3,4-x=0
=>x=3,4
Vậy GTLN của A = 0,5 khi x=3,4

\(A=\frac{2017^{2016-1}}{2017^{2017-1}}=\frac{2017^{2015}}{2017^{2016}}=\frac{2017^{2015}}{2017^{2015}.2017}=\frac{1}{2017}\)(1)
\(B=\frac{2017^{2015+1}}{2017^{2016+1}}=\frac{2017^{2016}}{2017^{2017}}=\frac{2017^{2016}}{2017^{2016}.2017}=\frac{1}{2017}\)(2)
Từ (1) và (2)\(\Rightarrow\)A = B

Thay x = 1 và y = -2 vào biểu thức M ta được
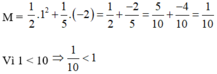
Vậy tại x = 1 và y = - 2 thì M < 1.
Chọn đáp án C

a) Vì \(\left|x-\frac{1}{3}\right|\ge0\forall x\)\(\Rightarrow\left|x-\frac{1}{3}\right|+\frac{1}{4}\ge\frac{1}{4}\forall x\)
hay \(P\ge\frac{1}{4}\)
mà \(\frac{1}{4}>\frac{1}{5}\)\(\Rightarrow P>\frac{1}{5}\)
b) Ta có: \(P\ge\frac{1}{4}\)( chứng minh phần a )
Dấu " = " xảy ra \(\Leftrightarrow x-\frac{1}{3}=0\)\(\Leftrightarrow x=\frac{1}{3}\)
Vậy \(minP=\frac{1}{4}\Leftrightarrow x=\frac{1}{3}\)
Xét hiệu A-B. Sau khi quy đồng ta được.
\(A-B=\frac{2013^{2015}-2013^{2014}-\left(2013^{2016}-2013^{2013}\right)}{\left(2013^{2016}-1\right)\left(2013^{2014}+1\right)}=\frac{2013^{2015}-2013^{2016}+2013^{2013}-2013^{2014}}{\left(2013^{2016}-1\right)\left(2013^{2014}+1\right)}< 0\)
Nên A<B.