
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2^195=(2^3)^65=8^65 ; 3^130=(3^2)^65=9^65
Mà 8<9 nên 8^65 < 9^65
=>2^195< 3^130
học tốt
Ta có:
\(2^{195}=\left(2^3\right)^{65}=8^{65}\)
\(3^{130}=\left(3^2\right)^{65}=9^{65}\)
Mà 8 < 9 nên \(8^{65}< 9^{65}\Rightarrow2^{195}< 3^{130}\)

a) 3^40= 3^4.10=(3^4)10=81^10
11^21> 11^20=11^2.10=(11^2)10=121^10
→ 3^40< 11^21
b) 2^195=2^15.13=(2^15)13=32768^13
3^130=3^10.13= (3^10)13=59049^13
→2^195<3^130
c) 2^90=2^5.18=(2^5)18= 32^18
5^36=5^2.18=(5^2)18=25^18
→2^90>5^36

2 ^ 90 = 2 ^ 10 x 9 = ( 2 ^ 10 ) ^ 9 = 1024 ^ 9
5 ^ 36 = 5 ^ 4 x 9 = ( 5 ^ 4 ) ^ 9 = 625 ^ 9
Vi 1024 > 625 nen 1024 ^ 9 > 625 ^ 9 hay 2 ^ 90 > 5 ^ 36
290=(25)18=3218
536=(52)18=2518
Vì 32>25 nên 3218>2518
Do đó 290>536
Kick cho mình nha!

\(2^{91}=2^{13.7}=8192^7\\ 5^{35}=5^{5.7}=3125^7\\ Vì:8192^7>3125^7\Rightarrow2^{91}>5^{35}\)

a) \(\frac{-7}{9}và\frac{3}{-8}\)
Ta có: \(\frac{-7}{9}=\frac{-56}{72}\)
\(\frac{3}{-8}=\frac{-3}{8}=\frac{-21}{72}\)
\(Vì\frac{-56}{72}< \frac{-21}{72}nên\frac{-7}{9}< \frac{3}{-8}\)
b)\(\frac{209}{310}và\frac{-718}{599}\)
Ta có: \(\frac{209}{310}>0\)
\(\frac{-718}{599}< 0\)
\(Vì\frac{209}{310}>0và\frac{-718}{599}< 0nên\frac{209}{310}>\frac{-718}{599}\)

a) xét \(\Delta HAC:\widehat{H}=90^o\)
\(\Rightarrow AH^2+HC^2=AC^2\)(đlý pytago)(1)
xét tam giác \(BHC:\widehat{H}=90^o\)
\(BH^2+HC^2=BC^2\)(đlý pytago)(2)
vì \(A\in BH\Rightarrow AH< BH\Rightarrow AH^2< BH^2\)(3)
từ (1);(2) và (3)
\(\Rightarrow BC^2>AC^2\Rightarrow BC>AC\)
b) xét tam giác \(AHD:\widehat{H}=90^o\)\(\Rightarrow AH^2+HD^2=AD^2\)(đ/lý pytago)(4)
lại có \(D\in HC\Rightarrow HD< HC\Rightarrow HD^2< HC^2\)(5)
từ (2);(4) và (5)
=>\(BC^2>AD^2\Rightarrow BC>AD\)
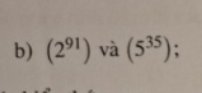
Ta có :
\(2^{195}=\left(2^3\right)^{65}=8^{65}\)
\(3^{130}=\left(3^2\right)^{65}=9^{65}\)
Ta thấy \(8^{65}< 9^{65}\)
=> \(2^{195}< 3^{130}\)