Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=-\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)...\left(1-\dfrac{1}{2014^2}\right)\)
\(A=\dfrac{\left(1\cdot3\right)\left(2\cdot4\right)\left(3\cdot5\right)...\left(2012\cdot2014\right)\left(2013\cdot2015\right)}{\left(2\cdot2\right)\left(3\cdot3\right)\left(4\cdot4\right)...\left(2013\cdot2013\right)\left(2014\cdot2014\right)}\)
\(A=\dfrac{\left(1\cdot2\cdot3\cdot...\cdot2012\cdot2013\right)\left(3\cdot4\cdot5\cdot...\cdot2014\cdot2015\right)}{\left(2\cdot3\cdot4\cdot...\cdot2013\cdot2014\right)\left(2\cdot3\cdot4\cdot...\cdot2013\cdot2014\right)}\)
\(A=\dfrac{1\cdot2015}{2014\cdot2}=\dfrac{2015}{4028}\)
Vì \(\dfrac{2015}{4028}>-\dfrac{1}{2}\) nên A > B

a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 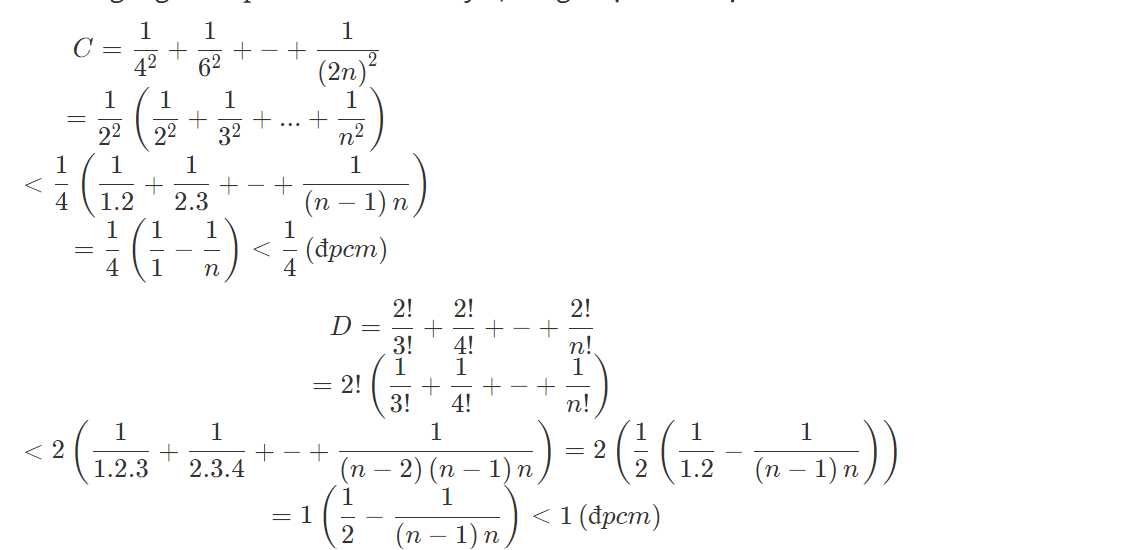

Đặt P= 1/4^2+1/6^2+1/8^2+...1/2n^2
= > P= 1/2.(2/2.4+2/4.6+2/6.8+...+ 2/(2n-2).2n)
=> P= 1/2.(1/2-1/2n)
=> P= 1/2.1/2-1/2.1/2n
=> P = (1/4 -1/2.1/2n)(1/4
Vậy P<1/4 ( đcpcm)

1/4^2+1/6^2+...+1/(2n)^2<1/4
=>1/2^2+1/3^2+...+1/n^2<1
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}< \dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{n\left(n-1\right)}=\dfrac{1}{2}-\dfrac{1}{n-1}< 1\)
=>ĐPCM

\(S=\dfrac{1}{2^2}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}\right)\)
=>\(S< =\dfrac{1}{4}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\right)\)
=>\(S< =\dfrac{1}{4}\cdot\left(1-\dfrac{1}{n}\right)=\dfrac{1}{4}\cdot\dfrac{n-1}{n}< =\dfrac{1}{4}\)

\(A=\dfrac{2}{4}.\left(\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{15}+...+\dfrac{1}{n}-\dfrac{1}{n+4}\right)\\ =\dfrac{2}{4}.\left(\dfrac{1}{3}-\dfrac{1}{n+4}\right)\\ =\dfrac{1}{2}.\dfrac{n+1}{3\left(n+4\right)}=\dfrac{n+1}{6\left(n+4\right)}\\ =\dfrac{n+4-3}{6\left(n+4\right)}=\dfrac{1}{6}-\dfrac{1}{2\left(n+4\right)}< \dfrac{1}{6}.\)
Giải:
A=2/3.7+2/7.11+2/11.15+...+2/n.(n+4)
A=1/2.(4/3.7+4/7.11+4/11.15+...+4/n.(n+4)
A=1/2.(1/3-1/7+1/7-1/11+1/11-1/15+...+1/n-1/n+4)
A=1/2.(1/3-1/n+4)
A=1/6-1/2.(n+4)
⇒A>1/6
Chúc bạn học tốt!

Ta có:\(\dfrac{1}{4^2}< \dfrac{1}{2.4}\)
\(\dfrac{1}{6^2}< \dfrac{1}{4.6}\)
\(\dfrac{1}{8^2}< \dfrac{1}{6.8}\)
...
\(\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{\left(2n-2\right).2n}\)
=>\(\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{2.4}+\dfrac{1}{4.6}+...+\dfrac{1}{\left(2n-2\right)2n}=\dfrac{1}{2}\cdot\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2n-2}-\dfrac{1}{2n}\right)=\dfrac{1}{2}\cdot\left(\dfrac{1}{2}-\dfrac{1}{2n}\right)< \dfrac{1}{2}\cdot\dfrac{1}{2}=\dfrac{1}{4}\left(đpcm\right)\)
Đặt A = \(\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+...+\dfrac{1}{\left(2n\right)^2}\)
\(A=\dfrac{1}{2^2}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}\right)\)
Đặt \(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}\)
Ta có :
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\) ( vì 1 > 0 ; 0 < 1.2 < 22 )
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\) ( vì 1 > 0 ; 0 < 2.3 < 32 )
\(\dfrac{1}{4^2}< \dfrac{1}{3.4}\) ( vì 1 > 0 ; 0 < 3.4 < 42 )
...
\(\dfrac{1}{n^2}< \dfrac{1}{\left(n-1\right)n}\) ( vì 1 > 0 ; 0 < ( n - 1 ) n < n2 )
\(\Rightarrow\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{\left(n-1\right)n}\)
\(\Rightarrow B< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(\Rightarrow B< 1-\dfrac{1}{n}< 1\Rightarrow A< 1.\dfrac{1}{4}\Rightarrow A< \dfrac{1}{4}\)

a/ Ta có :
\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...........+\dfrac{1}{n^2}\)
Ta thấy :
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
.......................
\(\dfrac{1}{n^2}< \dfrac{1}{\left(n-1\right)n}\)
\(\Leftrightarrow A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...........+\dfrac{1}{\left(n-1\right)n}\)
\(\Leftrightarrow A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+..........+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(\Leftrightarrow A< 1-\dfrac{1}{n}< 1\)
\(\Leftrightarrow A< 1\)
b/ Ta có :
\(B=\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+.................+\dfrac{1}{\left(2n\right)^2}\)
\(=\dfrac{1}{4}\left(1+\dfrac{1}{2^2}+\dfrac{1}{4^2}+..........+\dfrac{1}{n^2}\right)\)
Ta thấy :
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
..................
\(\dfrac{1}{n^2}< \dfrac{1}{\left(n-1\right)n}\)
\(\Leftrightarrow B< \dfrac{1}{4}\left(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+.........+\dfrac{1}{\left(n-1\right)n}\right)\)
\(\Leftrightarrow B< \dfrac{1}{4}\left(1+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+......+\dfrac{1}{n-1}-\dfrac{1}{n}\right)\)
\(\Leftrightarrow B< \dfrac{1}{4}\left(1+1-\dfrac{1}{n}\right)\)
\(\Leftrightarrow B< \dfrac{1}{2}-\dfrac{1}{4n}< \dfrac{1}{2}\)
\(\Leftrightarrow B< \dfrac{1}{2}\)
\(\)\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}\)
\(A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{\left(n-1\right)n}\)
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(A< 1-\dfrac{1}{n}< 1\)
\(B=\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2n^2}\)
\(B=\dfrac{1}{2}\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2n^2}\right)\)
\(B=\dfrac{1}{4}+\dfrac{1}{2}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2n^2}\right)\)
\(B< \dfrac{1}{4}+\dfrac{1}{2}\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+.....+\dfrac{1}{\left(n-1\right)n}\right)\)

Lời giải:
Ta có:
\(N=\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+...+\frac{1}{(2n)^2}< \frac{1}{4^2-1}+\frac{1}{6^2-1}+\frac{1}{8^2-1}+...+\frac{1}{(2n)^2-1}(*)\)
Mà:
\(\frac{1}{4^2-1}+\frac{1}{6^2-1}+\frac{1}{8^2-1}+...+\frac{1}{(2n)^2-1}=\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.9}+...+\frac{1}{(2n-1)(2n+1)}\)
\(=\frac{1}{2}\left(\frac{5-3}{3.5}+\frac{7-5}{5.7}+\frac{9-7}{7.9}+...+\frac{(2n+1)-(2n-1)}{(2n-1)(2n+1)}\right)\)
\(=\frac{1}{2}\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+....+\frac{1}{2n-1}-\frac{1}{2n+1}\right)=\frac{1}{2}\left(\frac{1}{3}-\frac{1}{2n+1}\right)\)
\(< \frac{1}{6}< \frac{1}{4}(**)\)
Từ \((*);(**)\Rightarrow N< \frac{1}{4}\) (đpcm)
Ta có :22A=1+\(\dfrac{1}{2^2}\)+\(\dfrac{1}{4^2}\)+...+\(\dfrac{1}{n^2}\)
22A-A=1-\(\dfrac{1}{\left(2n\right)^2}\)
3A=\(\dfrac{\left(2n\right)^2-1}{\left(2n\right)^2}\) <\(\dfrac{n^2}{\left(2n\right)^2}\)=\(\dfrac{1}{2}\)
3A<\(\dfrac{1}{2}\) suy ra A<\(\dfrac{1}{2}\)
A = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{4^2}\) + \(\dfrac{1}{6^2}\)+.......+\(\dfrac{1}{\left(2.n\right)^2}\)
A = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{\left(2.2\right)^2}\)+ \(\dfrac{1}{\left(2.3\right)^2}\) +....+\(\dfrac{1}{\left(2.n\right)^2}\)
A = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{2^2.2^2}\) + \(\dfrac{1}{2^2.3^2}\)+......+ \(\dfrac{1}{2^2.n^2}\)
A = \(\dfrac{1}{2^2}\) \(\times\) ( 1 + \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\)+.......+ \(\dfrac{1}{n^2}\))
22 \(\times\) A = 1 + \(\dfrac{1}{2^2}\)+ \(\dfrac{1}{3^2}\)+......+\(\dfrac{1}{n^2}\)
4A = 1 + \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) +......+ \(\dfrac{1}{n^2}\)
4A = 1 + \(\dfrac{1}{2.2}\) + \(\dfrac{1}{3.3}\) + ...+\(\dfrac{1}{n.n}\)
1 = 1
\(\dfrac{1}{2.2}\) < \(\dfrac{1}{1.2}\)
\(\dfrac{1}{3.3}\) < \(\dfrac{1}{2.3}\)
...................
\(\dfrac{1}{n.n}\) < \(\dfrac{1}{\left(n-1\right).n}\)
Cộng vế với vế ta có:
4A = 1+\(\dfrac{1}{2.2}\)+\(\dfrac{1}{3.3}\)+....+\(\dfrac{1}{n.n}\) <1+ \(\dfrac{1}{1.2}\)+ \(\dfrac{1}{2.3}\)+ ......+ \(\dfrac{1}{\left(n-1\right).n}\)
4A < 1+ \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\)+ \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)+....+\(\dfrac{1}{n-1}\) - \(\dfrac{1}{n}\) = 2 - \(\dfrac{1}{n}\)
A < ( 2 - \(\dfrac{1}{n}\)): 4
A < 2 : 4 - \(\dfrac{1}{n}\) : 4
A < \(\dfrac{1}{2}\) - \(\dfrac{1}{4n}\) < \(\dfrac{1}{2}\)
Vậy A < \(\dfrac{1}{2}\)