K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
M
2
6 tháng 3 2023
\(\dfrac{2001+2002}{2002+2003}< \dfrac{2001}{2002}+\dfrac{2002}{2003}\)
HT
2
29 tháng 6 2015
a) Ta có: \(1-\frac{2002}{2003}=\frac{1}{2003}\)
\(1-\frac{2003}{2004}=\frac{1}{2004}\)
Vì \(\frac{1}{2003}>\frac{1}{2004}\)
\(\Rightarrow\frac{2002}{2003}>\frac{2003}{2004}\)
b) Ta có: \(\frac{-2005}{-2004}=\frac{2005}{2004}>1\)
\(\frac{-2002}{2003}
KL
4
24 tháng 10 2021
\(\Rightarrow2A=2+2^2+2^3+...+2^{2003}\\ \Rightarrow2A-A=2+2^2+2^3+...+2^{2003}-1-2-...-2^{2002}\\ \Rightarrow A=2^{2003}-1=B\)
OM
28 tháng 12 2015
ai có lòng tick tôi lên 15 tôi cảm ơn nếu ko tick thì số đen sẽ đến với bn
M
2
B
11 tháng 5 2019
A = 1 + 2 + 22 + 23 + ... + 22002
=> 2A = 2 + 22 + 23 + 24 + ... + 22003
=> 2A - A = ( 2 + 22 + 23 + 24 + ... + 22003 ) - ( 1 + 2 + 22 + 23 + ... + 22002 )
A = 22003 - 1 < 22003
hay A < B
Vậy ...
11 tháng 5 2019
\(A=1+2+2^2+2^3+...+2^{2002}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{2002}+2^{2003}\)
\(\Rightarrow2A-A=2^{2003}-1\)
\(\Rightarrow A=2^{2003}-1\)
Vì \(2^{2003}-1< 2^{2003}\)
nên A < B
PV
2 tháng 3 2016
Có:
- 2003A=20032004+2003/20032004+1 = 20032004+1+2002/20032004+1= 1+ 2002/20032004+1
- 2003A= 20032003+2003/20032003+1 .........= 1 + 2002/20032003+1
- Vì 1+ 2002/20032004+1<1+ 20022003+1nên 2003A<2003B
- Nên A<B
- !!!!!!!!!!!
TT
2
27 tháng 1 2017
A = 1 + 2 + 22 + ... + 22002
=> 2A = 2(1 + 2 + 22 + ... + 22002 )
= 2 + 22 + 23 + .... + 22003
2A - A = ( 2 + 22 + 23 + .... + 22003 ) - ( 1 + 2 + 22 + ... + 22002 )
A = 22003 - 1
Vì 22003 - 1 < 22003 nên A < B
Vậy A < B
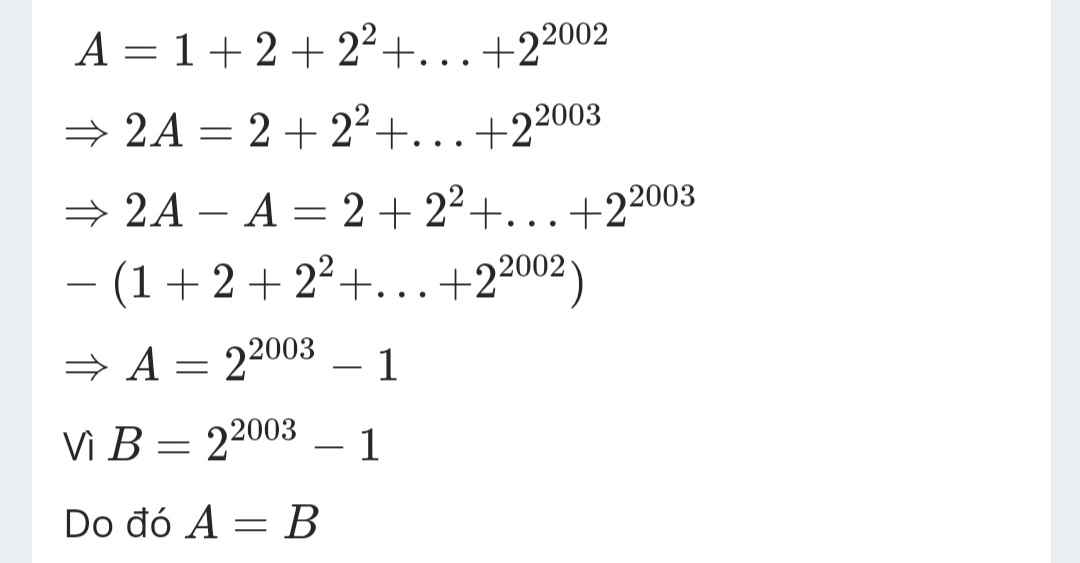
Ta có \(B=2002^2\)
\(=2002.2002\)
\(=2002.\left(2003-1\right)\)
\(=2002.2003-2002>2003.2002-2003=2001.2003\)
Khi đó A < B
Vậy....
Mình cảm ơn nha :3