LP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
7 tháng 8 2017
Đáp án A
Ta có: 2011 2012 + 2012 2013 + 2013 2011 = 2012 - 1 2012 + 2013 - 1 2013 + 2011 + 1 + 1 2011
= 1 - 1 2012 + 1 - 1 2013 + 1 + 1 2011 + 1 + 1 2011
= 3 + 1 2011 - 1 2012 + 1 2011 - 1 2013
Ta thấy vì 2011 < 2012 < 2013 nên 1 2011 > 1 2012 > 1 2013
Suy ra: 1 2011 - 1 2012 > 0 ; 1 2011 - 1 2012 > 0
Do đó: 3 + 1 2011 - 1 2012 + 1 2011 - 1 2013 > 3
Hay . 2011 2012 + 2012 2013 + 2013 2011 > 3
Đáp án cần chọn là: A
PT
1
OC
0
PT
1
PT
1
DL
1
AH
Akai Haruma
Giáo viên
2 tháng 2 2023
Lời giải:
Nếu $n$ chẵn thì vì $2012^{2013}$ chẵn nên $n+2012^{2013}$ chẵn
$\Rightarrow C$ chẵn (vì chứa thừa số chẵn)
Nếu $n$ lẻ thì vì $2013^{20120}$ lẻ nên $n+2013^{20120}$ chẵn
$\Rightarrow C$ chẵn (vì chứa thừa số chẵn)
Vậy trong mọi TH thì $C$ đều chẵn, tức là $C\vdots 2$ (đpcm)
PT
1
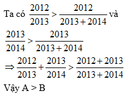
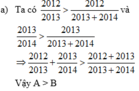
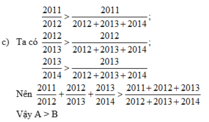
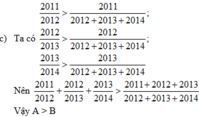
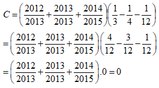
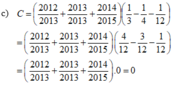
Có A=20122013+2/20122013-1
=(20122013-1)+3/20122013-1
=20122013-1/20122013-1 + 3/20122013-1
=1 + 3/20122013-1
Có B=20122013/20122013-3
=(20122013-3)+3/20122013-3
=20122013-3/20122013-3 + 3/20122013-3
=1 + 3/20122013-3
Vì 1 + 3/20122013-1>1+20122013-3
nên A>B
Vậy A>B