
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: 43/52>26/52=1/2=60/120
b: 17/68=1/4<1/3=35/105<35/103
c: \(\dfrac{2018\cdot2019-1}{2018\cdot2019}=1-\dfrac{1}{2018\cdot2019}\)
\(\dfrac{2019\cdot2020-1}{2019\cdot2020}=1-\dfrac{1}{2019\cdot2020}\)
2018*2019<2019*2020
=>-1/2018*2019<-1/2019*2020
=>\(\dfrac{2018\cdot2019-1}{2018\cdot2019}< \dfrac{2019\cdot2020-1}{2019\cdot2020}\)

\(\dfrac{19}{19}\) = 1 < \(\dfrac{2005}{2004}\) vậy \(\dfrac{19}{19}\) < \(\dfrac{2005}{2004}\)
\(\dfrac{72}{73}\) = 1 - \(\dfrac{1}{73}\)
\(\dfrac{98}{99}\) = 1 - \(\dfrac{1}{99}\)
Vì \(\dfrac{1}{73}\) > \(\dfrac{1}{99}\) nên \(\dfrac{72}{73}\) < \(\dfrac{98}{99}\)

a) ta có: \(1-\frac{2012}{2013}=\frac{1}{2013}\)
\(1-\frac{2013}{2014}=\frac{1}{2014}\)
mà \(\frac{1}{2013}>\frac{1}{2014}\) nên \(\frac{2013}{2014}>\frac{2012}{2013}\)

2225 = (23)75 = 875
3151 > 3150 = (32)75 = 975
=> 3151 > 975 > 875
=> 3151 > 2225
4n - 5 chia hết cho 2n - 1
=> 4n - 2 - 3 chia hết cho 2n - 1
=> 2.(2n - 1) - 3 chia hết cho 2n - 1
Do 2.(2n - 1) chia hết cho 2n - 1 => 3 chia hết cho 2n - 1
Mà n thuộc N => 2n - 1 > hoặc = -1
=> 2n - 1 thuộc {-1 ; 1 ; 3}
=> 2n thuộc {0 ; 2 ; 4}
=> n thuộc {0 ; 1 ; 2}

Hướng dẫn: Cách làm là chuyển số thập phân thành phân số (bằng cách nhân với 100) và chuyển hỗn số thành phân số, sau đó thực hiện phép tính.
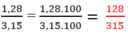

Hướng dẫn: Cách làm là chuyển số thập phân thành phân số (bằng cách nhân với 100) và chuyển hỗn số thành phân số, sau đó thực hiện phép tính.
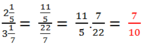

Ta thấy : \(2222^{3333}vs2^{300}:\hept{\begin{cases}2222>2\\3333>300\end{cases}\Rightarrow2222^{3333}>2^{300}}\)
Ta thấy : \(2222^{1111}=1111^{1111}.2^{1111}< 1111^{1111}.1111^{1110}=1111^{2221}\)
Ta thấy : \(54^{10}=\left(3^3\right)^{10}.2^{10}=3^{30}.2^{10}=3^{12}.3^{18}.2^{10}>3^{12}.7^{12}=21^{12}.\)
\(17^{20}=\left(17^4\right)^5=83521^5\)
\(31^{15}=\left(31^3\right)^5=29719^5\)
Vậy: \(17^{20}>31^{15}\)
1720 > 1620 = 165 . 1615 = (24)5 . 1615 = 220 . 1615 > 215 . 1615 = 3215 > 3115