
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) Đặt x 2 = t (t ≥ 0). Khi đó ta có phương trình: t 2 – mt – m – 1 = 0 (*)
Δ = m 2 - 4(-m - 1) = m 2 + 4m + 4 = m + 2 2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
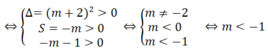


25x2 + 10x + 1 = 0
Có a = 25 ; b = 10 ; c = 1
Δ = b2 – 4ac = 102 – 4.25.1 = 0
Khi đó theo hệ thức Vi-et có:
x1 + x2 = -b/a = -10/25 = -2/5
x1.x2 = c/a = 1/25.

Phương trình (1) vô nghiệm khi phương trình (2) có 2 nghiệm số âm hoặc vô nghiệm.
Nếu phương trình (2) có 2 nghiệm âm thì theo hệ thức Vi-ét ta có:
t 1 + t 2 = 13 > 0 vô lý
Vậy phương trình (1) vô nghiệm khi phương trình (2) vô nghiệm.
Suy ra: ∆ = 169 - 4m < 0 ⇔ m > 169/4}

Phương trình (1) có một nghiệm khi phương trình (2) có 1 nghiệm số kép bằng 0 hoặc phương trình (2) có một nghiệm bằng 0 và một nghiệm số âm.
Ta thấy, với ∆ = 0 phương trình (2) có nghiệm số kép t 1 = t 2 = 13/2 ≠ 0( không thỏa mãn)
Nếu phương trình (2) có một nghiệm t1 = 0. Theo hệ thức Vi-ét ta có:
t 1 + t 2 = 13 ⇔ t 2 = 13 - t 1 = 13 - 0 = 13 > 0 ( không thỏa mãn)
Vậy không có giá trị nào của m để phương trình (1) chỉ có 1 nghiệm.


Phương trình (1) có ba nghiệm phân biệt khi phương trình (2) có 1 nghiệm số dương và 1 nghiệm bằng 0 khi:
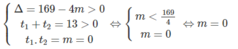


Phương trình (1) có hai nghiệm phân biệt khi phương trình (2) có nghiệm kép hoặc có 1 nghiệm dương và một nghiệm âm.
Phương trình (2) có một nghiệm số kép khi và chỉ khi Δ = 169 - 4m = 0
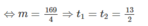
Phương trình (2) có một nghiệm số dương và một nghiệm số âm khi
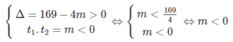
Vậy với m = 169/4 hoặc m < 0 thì phương trình (1) có 2 nghiệm phân biệt.

4 nghiệm
-1; 2; 3; 6
https://h.vn/hoi-dap/question/238231.html?pos=815256