Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B.
Các giá trị khác nhau của dấu hiệu trên là: 98; 99; 101; 102; 103; 104; 106; 107; 108; 109; 111; 112; 113; 114; 115; 118; 122; 124; (Có 18 giá trị khác nhau của dấu hiệu)
Chọn A.
Giả sử các giá trị của mẫu số liệu là a; b; c; d với 0 < a < b < c < d và a; b; c;d là số tự nhiên.
+ Ta có 
Mà số trung bình là 6 nên a + b + c + d = 24
Suy ra a + d = 14
+ Ta có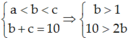 
hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
+ Nếu b = 2 thì c = 8, mà 0 < a < b; a là số tự nhiên nên a = 1 và d = 13
Khi đó các giá trị của mẫu số liệu là 1; 2; 8; 13
+ Nếu b = 3 thì c = 7, mà 0 < a < b; a số tự nhiên nên có 2 khả năng xảy ra: a = 1 ; d = 13 hoặc a = 2 ; d = 12
Khi đó có hai mẫu số liệu thỏa đề bài có giá trị là 1;3;7;13 và 2;3;7;12
+ Nếu b = 4 thì c = 6, mà 0 < a < b; a là số tự nhiên nên có 3 khả năng xảy ra:
a = 1; d = 13 hoặc a = 2 ; d = 12 hoặc a = 3 ; d = 11
Khi đó có ba mẫu số liệu thỏa đề bài có giá trị là 1;4;6;13 hoặc 2;4;6;12 hoặc 3;4;6;11
Suy ra với mẫu số liệu có các giá trị là 3;4;6;11 thì hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.
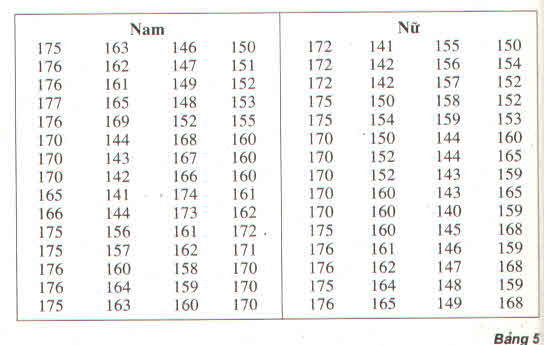
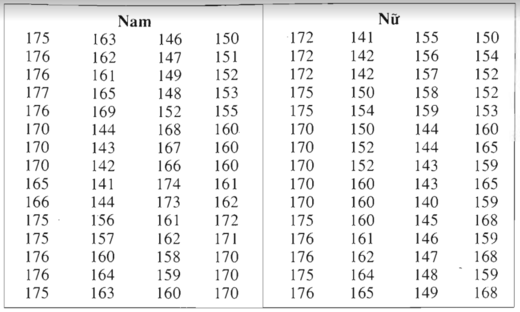
a) Tính chiều cao trung bình của học sinh nam
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp :
\(\overline{x}=\dfrac{1}{60}\left(5.140+9.150+19.160+17.170+10.180\right)\)
\(\overline{x}=163\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(8,33.140+15.150+31,67.160+28,33.170+16,67.180\right)\)\(\overline{x}=163\)
Tính chiều cao trung bình của học sinh nữ:
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp \(\overline{x}=\dfrac{1}{60}\left(8.140+15.150+16.160+14.170+7.180\right)\)
\(\overline{x}=159,5\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(13,33.140+25.150+26,67.160+23,33.170+11,67.180\right)\)
\(\overline{x}=159,5\)
b) Vì \(\overline{x}_{nam}=163>\overline{x}_{nữ}=159,5\) nên suy ra học sinh ở nhóm nam cao hơn học sinh ở nhóm nữ
c) \(\overline{x}=\left(60.159,5+60.163\right)\dfrac{1}{2}\approx161\left(cm\right)\)
• Ta có:
- Số trung bình cộng x = 55,82 trường là không có nghĩa.
- Trong các số liệu thống kê đã cho có sự chênh lệch quá lớn (điều này chứng tỏ các số liệu thống kê đã cho là không cùng loại)
Chỉ cần một trong hai điều kể trên là đủ để suy ra rằng: Không chọn được số trung bình cộng làm đại diện cho các số liệu thống kê.
• Dễ thấy: Bảng số liệu thống kê đã cho không có mốt.
• Trong trường hợp đã cho, ta chọn số trung vị M e = 40 (trường) để làm đại diện cho các số liệu thống kê đã cho (về quy mô và độ lớn).
Đáp án: B
Chọn B
Lập bảng tần số- tần suất:
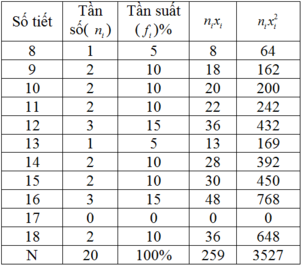
Số trung bình của dãy số liệu trên là:
x ¯ = ∑ . n i . x i N = 259 20 = 12 , 59
Trong số học sinh có chiều cao chưa đến 155 cm, học sinh nữ đông hơn học sinh nam.
Dấu hiệu là học sinh giỏi, đơn vị điều tra là mỗi lớp của trường THPT
Kích thước mẫu là 30
Chọn D.
Dựa vào bảng thống kê trên ta thấy: các giá trị khác nhau của mẫu số liệu trên là 0;1;2;3;4;5;6.
Chọn C