K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PP
7 tháng 5 2021
2A=2*(1+2+22+...+22020)=2+22+...+22021
2A-A=(1+2+22+...+22021)-(1+2+22+...+22020)
A=22021-1<2021
8 tháng 5 2021
Giải:
A=1+2+22+23+...+22020
2A=2+22+23+24+...+22021
2A-A=(2+22+23+24+...+22021)-(1+2+22+23+...+22020)
A=22021-1
⇒A<22021
Chúc bạn học tốt!
PK
1
11 tháng 5 2023
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\)
\(\Rightarrow\dfrac{1}{2}A=\dfrac{1}{2}.\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\right)\)\(\Rightarrow\dfrac{1}{2}A=\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\)
\(\Rightarrow A-\dfrac{1}{2}A=\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\right)-\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\right)\)\(\Rightarrow\dfrac{1}{2}A=\dfrac{1}{2}-\dfrac{1}{2^{2022}}\)
\(\Rightarrow\dfrac{1}{2}A=\dfrac{2^{2021}-1}{2^{2022}}\)
\(\Rightarrow A=\dfrac{2^{2021}-1}{2^{2023}}.2=\dfrac{2^{2021}-1}{2^{2021}}\)
Vậy \(A=\dfrac{2^{2021}-1}{2^{2021}}\)
NT
1
18 tháng 4 2022
A=1/2+1/22+1/23+...+1/22020+1/22021 > B=1/3+1/4+1/5+13/60
9 tháng 2 2022
Bài 2:
a: =>x-45=-20
hay x=25
b: =>35+30-5x=-12+112
=>65-5x=100
=>5x=-35
hay x=-7
c: =>x-124=1000
hay x=1124
d: \(\Leftrightarrow46-\left(3x-2\right)^3=-18\)
\(\Leftrightarrow\left(3x-2\right)^3=64\)
=>3x-2=4
hay x=2
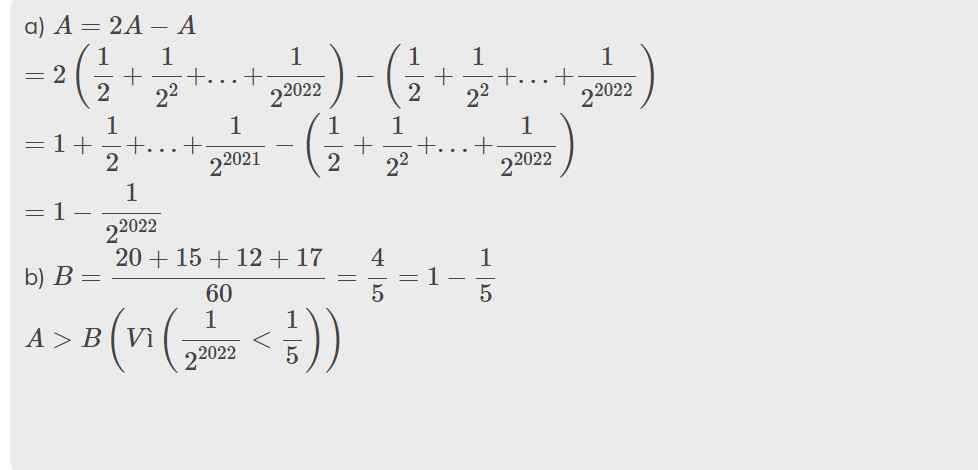
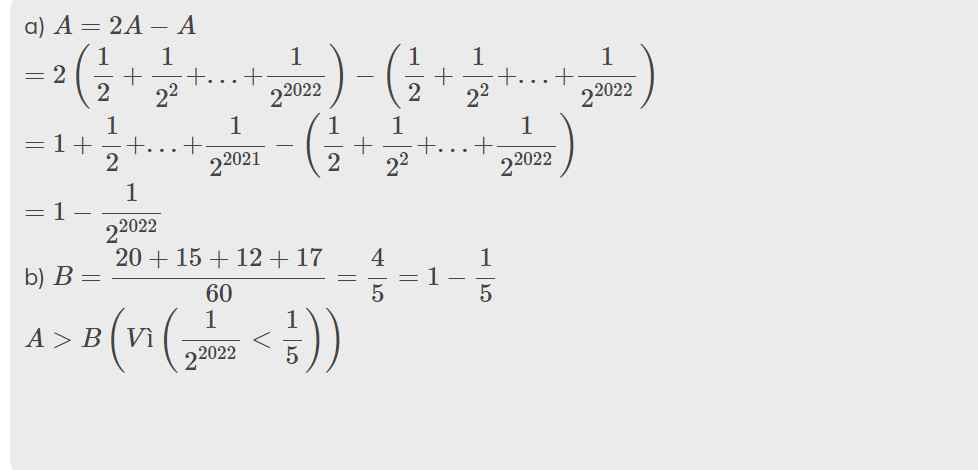
\(2S=2+2^2+...+2^{2022}\\ \Leftrightarrow2S-S=S=2^{2022}-1\)