TL
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KT
2
22 tháng 2 2021
Ta có: \(\dfrac{x^{24}+x^{20}+x^{16}+...+x^4+1}{x^{26}+x^{24}+x^{22}+...+x^2+1}\)
\(=\dfrac{x^{24}+x^{20}+x^{16}+...+x^4+1}{\left(x^{26}+x^{22}+...+x^2\right)+\left(x^{24}+x^{20}+x^{16}+...+x^4+1\right)}\)
\(=\dfrac{x^{24}+x^{20}+x^{16}+...+x^4+1}{x^2\left(x^{24}+x^{20}+...+1\right)+\left(x^{24}+x^{20}+x^{16}+...+x^4+1\right)}\)
\(=\dfrac{x^{24}+x^{20}+x^{16}+...+x^4+1}{\left(x^{24}+x^{20}+x^{16}+...+1\right)\left(x^2+1\right)}\)
\(=\dfrac{1}{x^2+1}\)
OH
22 tháng 2 2021
x24+x20+x16+...+x4+1x26+x24+x22+...+x2+1x24+x20+x16+...+x4+1x26+x24+x22+...+x2+1
=x24+x20+x16+...+x4+1(x26+x22+...+x2)+(x24+x20+x16+...+x4+1)=x24+x20+x16+...+x4+1(x26+x22+...+x2)+(x24+x20+x16+...+x4+1)
=x24+x20+x16+...+x4+1x2(x24+x20+...+1)+(x24+x20+x16+...+x4+1)=x24+x20+x16+...+x4+1x2(x24+x20+...+1)+(x24+x20+x16+...+x4+1)
=x24+x20+x16+...+x4+1(x24+x20+x16+...+1)(x2+1)
AN
27 tháng 10 2018
\(\dfrac{x^{24}+x^{20}+x^{16}+...+x^4+1}{x^{26}+x^{24}+x^{22}+...+x^2+1}\)
\(=\dfrac{x^{24}+x^{20}+x^{16}+...+x^4+1}{\left(x^{26}+x^{22}+x^{18}+...+x^2\right)+\left(x^{24}+x^{20}+x^{16}+...+1\right)}\)
\(=\dfrac{x^{24}+x^{20}+x^{16}+...+x^4+1}{x^2\left(x^{24}+x^{20}+x^{16}+...+1\right)+\left(x^{24}+x^{20}+x^{16}+...+1\right)}\)
\(=\dfrac{x^{24}+x^{20}+x^{16}+...+x^4+1}{\left(x^2+1\right)\left(x^{24}+x^{20}+x^{16}+...+1\right)}\)
\(=\dfrac{1}{x^2+1}\)
ND
Rút gọn phân thức:
A=\(\frac{x^{24}+x^{20}+x^{16}+.....+x^4+1}{x^{26}+x^{24}+x^{22}+.......+x^2+1}\)
1
18 tháng 1 2017
\(A=\frac{x^{24}+x^{20}+x^{16}+....+x^4+1}{x^{26}+x^{24}+x^{22}+.....+x^2+1}\) (1)
Ta có \(x^{26}+x^{24}+x^{22}+...+x^2+1\)
\(=\left(x^{26}+x^{22}+x^{18}+....+x^2\right)+\left(x^{24}+x^{20}+...+x^4+1\right)\)
\(=x^2\left(x^{24}+x^{20}+.....+x^4+1\right)+\left(x^{24}+x^{20}+...+x^4+1\right)\)
\(=\left(x^2+1\right)\left(x^{24}+x^{20}+x^{16}+....+x^4+1\right)\) (2)
Từ (1),(2) ta có \(A=\frac{x^{24}+x^{20}+x^{16}+...+x^4+1}{\left(x^2+1\right)\left(x^{24}+x^{20}+x^{16}+....+x^4+1\right)}=\frac{1}{x^2+1}\)
Vậy A=\(\frac{1}{x^2+1}\)
NH
0
NM
1
10 tháng 1 2018
Ta có:
\(\dfrac{x^{24}+x^{20}+x^{16}+x^{12}+...+x^4+1}{x^{26}+x^{24}+x^{22}+x^{20}+...+x^2+1}\)
Xét \(M=x^{24}+x^{20}+x^{16}+x^{12}+...+x^4+1\)
\(\Rightarrow x^4M=x^{28}+x^{24}+x^{20}+x^{16}+...+x^8+x^4\)
\(\Rightarrow x^4M-M=\left(x^{28}+x^{24}+x^{20}+...+x^8+x^4\right)-\left(x^{24}+x^{20}+x^{16}+...+x^4+1\right)\)
\(\Rightarrow\left(x^4-1\right)M=x^{28}-1\)
\(\Rightarrow M=\dfrac{x^{28}-1}{x^4-1}\)
Xét \(N=x^{26}+x^{24}+x^{22}+x^{20}+...+x^2+1\)
\(\Rightarrow x^2N=x^{28}+x^{26}+x^{24}+x^{20}+...+x^4+x^2\)
\(\Rightarrow x^2N-N=\left(x^{28}+x^{26}+x^{24}+...+x^4+x^2\right)-\left(x^{26}+x^{24}+x^{22}+...+x^2+1_{ }\right)\)
\(\Rightarrow\left(x^2-1\right)N=x^{28}-1\)
\(\Rightarrow N=\dfrac{x^{28}-1}{x^2-1}\)
Ta có:
\(\dfrac{x^{24}+x^{20}+x^{16}+x^{12}+...+x^4+1}{x^{26}+x^{24}+x^{22}+x^{20}+...+x^2+1}\)
\(=\dfrac{M}{N}=\dfrac{\dfrac{x^{28}-1}{x^4-1}}{\dfrac{x^{28}-1}{x^2-1}}\)
\(=\dfrac{x^{28}-1}{x^4-1}.\dfrac{x^2-1}{x^{28}-1}=\dfrac{x^2-1}{x^4-1}\)
\(=\dfrac{x^2-1}{\left(x^2-1\right)\left(x^2+1\right)}=\dfrac{1}{x^2+1}\)
Chúc bạn học tốt!
17 tháng 7 2021
1) Ta có: \(\left(x+2\right)^2+\left(x-3\right)^2\)
\(=x^2+4x+4+x^2-6x+9\)
\(=2x^2-2x+13\)
2) Ta có: \(\left(4-x\right)^2-\left(x-3\right)^2\)
\(=\left(4-x-x+3\right)\left(4-x+x-3\right)\)
\(=-2x+7\)
3) Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x+5\right)^2\)
\(=x^2-25-x^2-10x-25\)
=-10x-50
17 tháng 7 2021
4) Ta có: \(\left(x-3\right)^2-\left(x-4\right)\left(x+4\right)\)
\(=x^2-6x+9-x^2+16\)
=-6x+25
5) Ta có: \(\left(y^2-6y+9\right)-\left(y-3\right)^2\)
\(=y^2-6y+9-y^2+6y-9\)
=0
6) Ta có: \(\left(2x+3\right)^2-\left(2x-3\right)\left(2x+3\right)\)
\(=4x^2+12x+9-4x^2+9\)
=12x+18
13 tháng 5 2022
a: \(=\dfrac{2^{19}\cdot3^9+2^{20}\cdot3^{10}}{2^{19}\cdot3^9+2^{18}\cdot3^9\cdot5}=\dfrac{2^{19}\cdot3^9\left(1+2\cdot3\right)}{2^{18}\cdot3^9\left(2+5\right)}=2\)
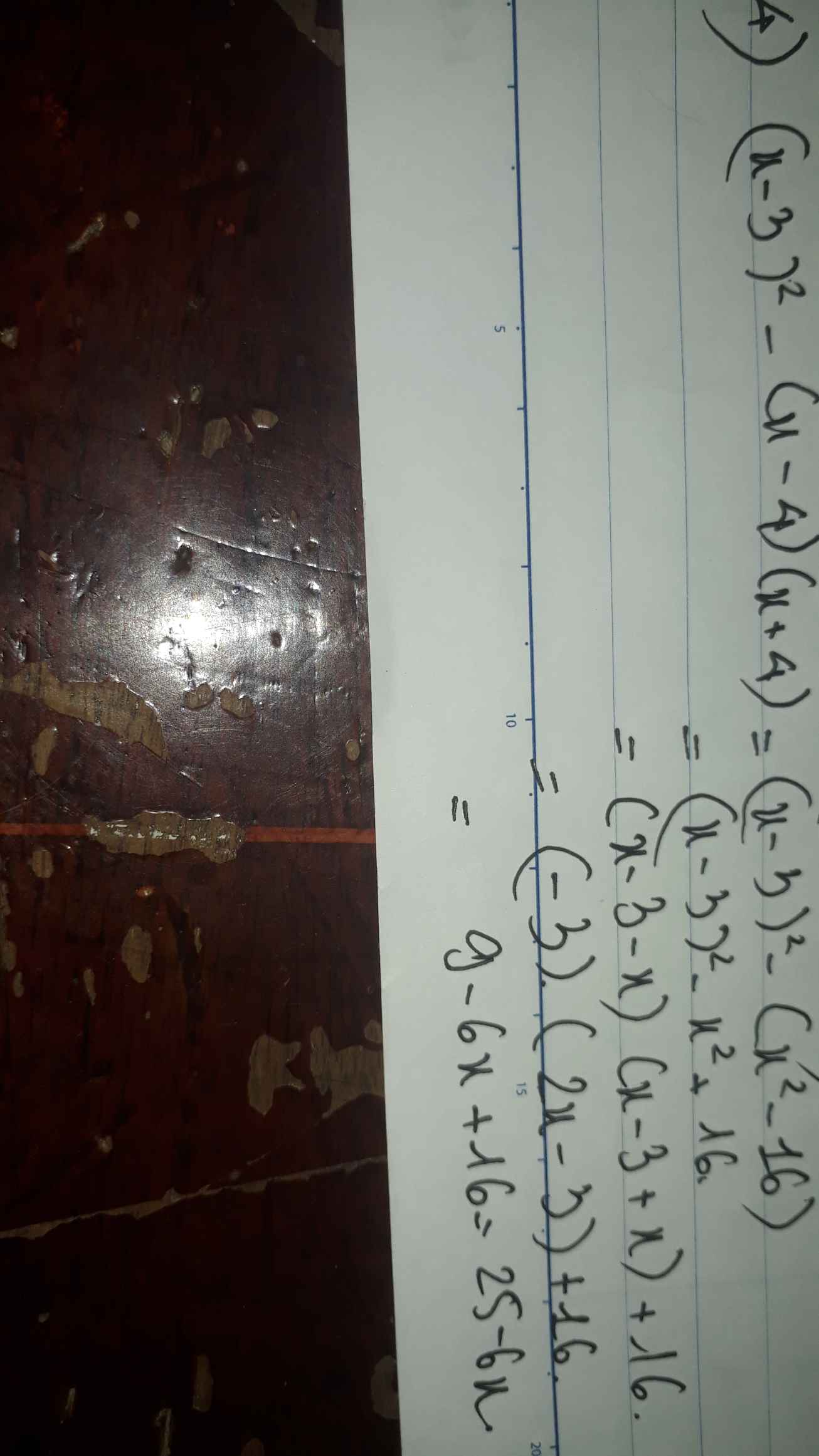
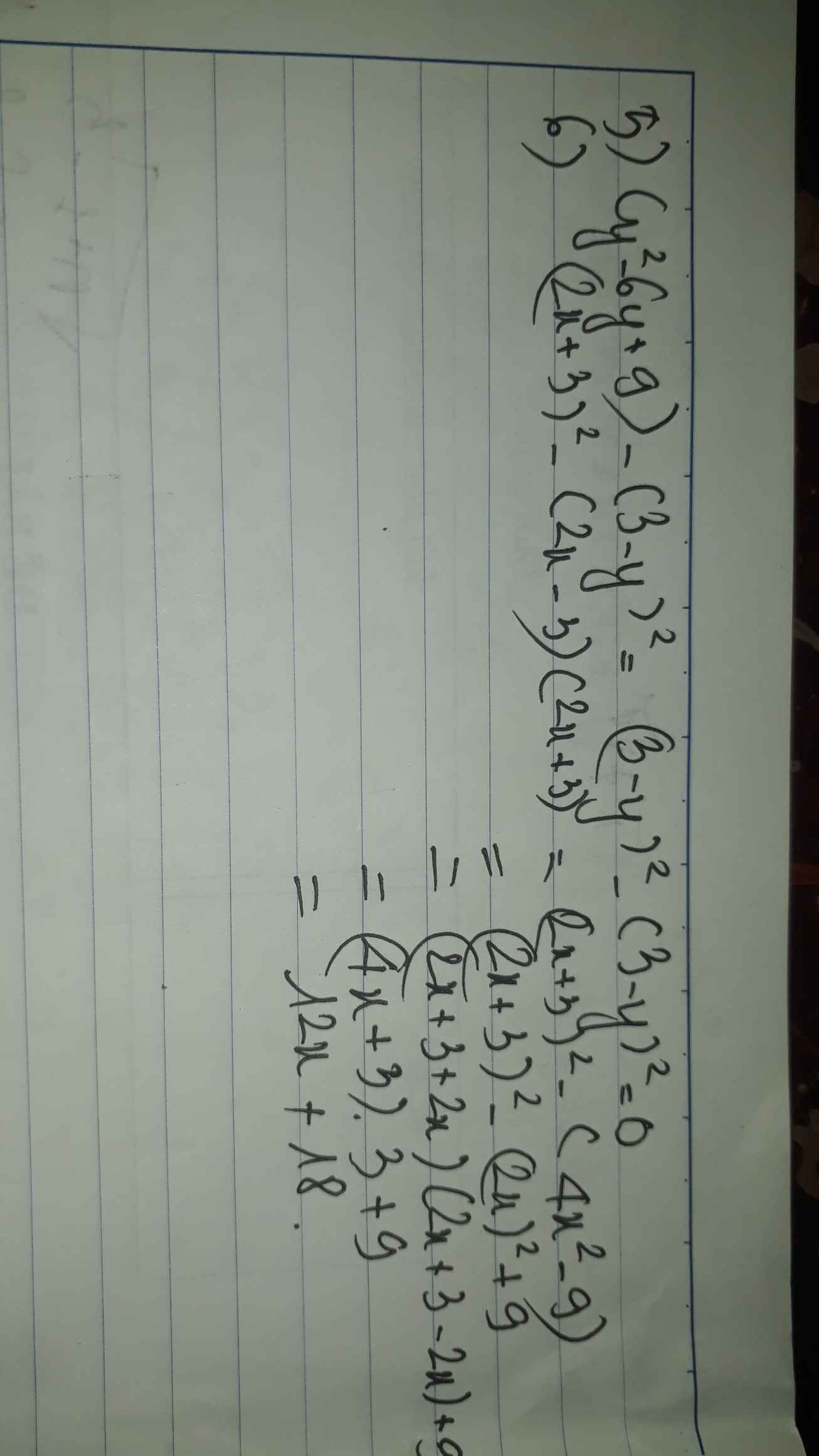
\(\frac{x^{24}+x^{20}+...+x^4+1}{x^{26}+x^{24}+...+x^2+1}=\frac{x^{24}+x^{20}+...+x^4+1}{\left(x^{24}+x^{20}+...+x^4+1\right)+\left(x^{26}+x^{22}+...+x^2\right)}\)
\(=1-\frac{x^2\left(x^{24}+x^{20}+...+x^4+x^1\right)}{\left(1+x^2\right)\left(x^{24}+2^{20}+...+x^4+1\right)}=1-\frac{x^2}{1+x^2}\)
\(=\frac{1+x^2-x^2}{1+x^2}=\frac{1}{1+x^2}\)
Hoặc cách khác:
\(\frac{x^{24}+x^{20}+...+x^4+1}{x^{26}+x^{24}+...+x^2+1}=\frac{x^{24}+x^{20}+...+x^4+1}{\left(x^{24}+x^{20}+...+x^4+1\right)+x^2\left(x^4+x^{20}+...+x^4+1\right)}\)
\(=\frac{x^{24}+x^{20}+...+x^4+1}{\left(x^2+1\right)\left(x^{24}+x^{20}+...+x^4+1\right)}=\frac{1}{x^2+1}\)