Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) = √4.
= 2(1 + 6x+
).
Tại x = -√2, giá trị của là 2(1 + 6(-√2) + 9(
= 2(1 - 6√2 +9.2)
= 2(19 - 6√2) ≈ 21,03.
b) =
= √9..
= 3.│a│.│b - 2│.
Tại a = -2 và b = -√3, giá trị của biểu thức là 3.│-2│.│-√3 - 2│= 3.2.(√3 + 2) = 6(√3 + 2) ≈ 22,392.
a) = √4.
= 2(1 + 6x+
).
Tại x = -√2, giá trị của là 2(1 + 6(-√2) + 9(
= 2(1 - 6√2 +9.2)
= 2(19 - 6√2) ≈ 21,03.
b) =
= √9..
= 3.│a│.│b - 2│.
Tại a = -2 và b = -√3, giá trị của biểu thức là 3.│-2│.│-√3 - 2│= 3.2.(√3 + 2) = 6(√3 + 2) ≈ 22,392.

a) \(\sqrt{4\left(1+6x+9x^2\right)^2}\) = \(\sqrt{\left(2\left(1+6x+9x^2\right)\right)^2}\)
= \(\sqrt{\left(2\left(1-6\sqrt{2}+18\right)\right)^2}\) = \(2\left(1-6\sqrt{2}+18\right)\) = \(2\left(3\sqrt{2}-1\right)^2\)
= \(21,029\)
b) \(\sqrt{9a^2\left(b^2+4-4b\right)}\) = \(\sqrt{\left(3a\left(b-2\right)\right)^2}\) = \(\sqrt{\left(-6\left(-\sqrt{3}-2\right)\right)^2}\)
= \(\sqrt{\left(6\sqrt{3}+12\right)^2}\) = \(6\sqrt{3}+12\) = \(22,392\)

a)\(A=\sqrt{2^2\left(1+6x+9x^2\right)^2}=2\left(1+6x+9x^2\right)\)
\(=2\left(3x+1\right)^2\).Tại \(x=-\sqrt{2}\) ta có:
\(=2\cdot\left(3\cdot-\sqrt{2}+1\right)^2=2\cdot\left(1-3\sqrt{2}\right)^2=2\cdot19-6\sqrt{2}=38-12\sqrt{2}\)
b)\(B=\sqrt{9a^2\left(b^2+4-4b\right)}=\sqrt{3^2a^2\left(b^2-2\cdot2\cdot b+2^2\right)}\)
\(=\sqrt{\left(3a\right)^2\left(b-2\right)^2}\)
\(=3\cdot a\cdot\left(b-2\right)\).Tại \(a=-2;b=-\sqrt{3}\) ta có:
\(B=3\cdot\left(-2\right)\cdot\left(-\sqrt{3}-2\right)=\left(-6\right)\cdot\left(-2-\sqrt{3}\right)=12+6\sqrt{3}\)
a) \(\sqrt{4\left(1+6x+9x^2\right)^2}=\sqrt{2^2.\left(3x+1\right)^4}=2.\left(3x+1\right)^2\)
Thay x vào và tính :)
b) \(\sqrt{9a^2\left(b^2-4b+4\right)}=\sqrt{\left(3a\right)^2.\left(b-2\right)^2}=\left|3a\right|.\left|b-2\right|\)
Thay a,b vào và tính :)

\(b.\)
\(=\sqrt{\left(3a\right)^2\cdot\left(b-2\right)^2}\)
\(=\left|3a\right|\cdot\left|b-2\right|\)
Với : \(a=2,b=-\sqrt{3}\)
\(2\cdot3\cdot\left(-\sqrt{3}-2\right)=6\cdot\left(-\sqrt{3}-2\right)\)

a) Ta có:
√4(1+6x+9x2)24(1+6x+9x2)2 =√4.√(1+6x+9x2)2=4.(1+6x+9x2)2
=√4.√(1+2.3x+32.x2)2=4.(1+2.3x+32.x2)2
=√22.√[12+2.3x+(3x)2]2=22.[12+2.3x+(3x)2]2
=2.√[(1+3x)2]2=2.[(1+3x)2]2
=2.∣∣(1+3x)2∣∣=2.|(1+3x)2|
=2(1+3x)2=2(1+3x)2.
(Vì (1+3x)2>0(1+3x)2>0 với mọi xx nên ∣∣(1+3x)2∣∣=(1+3x)2|(1+3x)2|=(1+3x)2)
Thay x=−√2x=−2 vào biểu thức rút gọn trên, ta được:
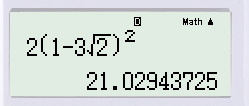
2[1+3.(−√2)]2=2(1−3√2)22[1+3.(−2)]2=2(1−32)2.
Bấm máy tính, ta được: 2(1−3√2)2≈21,0292(1−32)2≈21,029.
b) Ta có:
√9a2(b2+4−4b)=√32.a2.(b2−4b+4)9a2(b2+4−4b)=32.a2.(b2−4b+4)
=√(3a)2.(b2−2.b.2+22)=(3a)2.(b2−2.b.2+22)
=√(3a)2.√(b−2)2=(3a)2.(b−2)2
=|3a|.|b−2|=|3a|.|b−2|
Thay a=−2a=−2 và b=−√3b=−3 vào biểu thức rút gọn trên, ta được:
|3.(−2)|.∣∣−√3−2∣∣=|−6|.∣∣−(√3+2)∣∣|3.(−2)|.|−3−2|=|−6|.|−(3+2)|
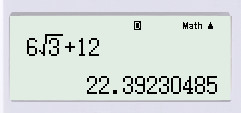
=6.(√3+2)=6√3+12=6.(3+2)=63+12.
Bấm máy tính, ta được: 6√3+12≈22,39263+12≈22,392.
a) Ta có:
.
(Vì với mọi nên )
Thay vào biểu thức rút gọn trên, ta được:
.
Bấm máy tính, ta được: .
b) Ta có:
Thay và vào biểu thức rút gọn trên, ta được:
.
Bấm máy tính, ta được: .

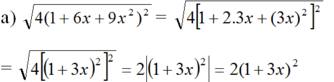
(vì (1 + 3x)2 > 0)
Thay x = √2 vào ta được:
2[1 + 3.(-√2)]2 = 2(1 - 3√2)2
= 2(1 - 6√2 + 32.2) = 2 - 12√2 + 36
= 38 - 12√2 = 38 - 12.1,414 = 38 - 16,968
= 21,032
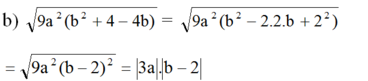
Thay a = -2, b = -√3 ta được:
|3(-2)|.|-√3 - 2| = 6(√3 + 2)
= 6(1,732 + 2) = 6.3,732
= 22,392
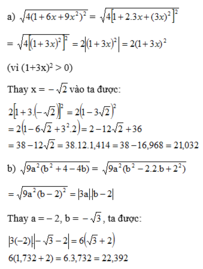

a) Ta có: \(A=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\right):\left(\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)
\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\)
\(=\dfrac{-3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{-3}{\sqrt{x}+3}\)
b) Để \(A< -\dfrac{1}{3}\) thì \(A+\dfrac{1}{3}< 0\)
\(\Leftrightarrow\dfrac{-3}{\sqrt{x}+3}+\dfrac{1}{3}< 0\)
\(\Leftrightarrow\dfrac{-9+\sqrt{x}+3}{3\left(\sqrt{x}+3\right)}< 0\)
\(\Leftrightarrow\sqrt{x}-6< 0\)
\(\Leftrightarrow x< 36\)
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0\le x< 36\\x\ne9\end{matrix}\right.\)

a) Ta có: \(\sqrt{27\cdot48\left(1-a^2\right)}\)
\(=\sqrt{3^4\cdot4^2\cdot\left(1-a^2\right)}\)
\(=36\sqrt{1-a^2}\)
c) Ta có: \(\sqrt{5a}\cdot\sqrt{45a}-3a\)
\(=15a-3a=12a\)
b) Ta có: \(B=\dfrac{1}{a-b}\cdot\sqrt{a^4\cdot\left(a-b\right)^2}\)
\(=\dfrac{1}{a-b}\cdot a^2\cdot\left(a-b\right)\)
\(=a^2\)
d) Ta có: \(D=\left(3-a\right)^2-\sqrt{0.2}\cdot\sqrt{180a^2}\)
\(=a^2-6a+9-\sqrt{36a^2}\)
\(=a^2-6a+9-\left|6a\right|\)
\(=\left[{}\begin{matrix}a^2-6a+9-6a\left(a\ge0\right)\\a^2-6a+9+6a\left(a< 0\right)\end{matrix}\right.\)
\(=\left[{}\begin{matrix}a^2-12a+9\\a^2+9\end{matrix}\right.\)

a: \(=\dfrac{4x-8\sqrt{x}+8x}{x-4}:\dfrac{\sqrt{x}-1-2\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4\sqrt{x}\left(3\sqrt{x}-2\right)}{x-4}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{-\sqrt{x}+3}=\dfrac{-4x\left(3\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}\)
b: \(m\left(\sqrt{x}-3\right)\cdot B>x+1\)
=>\(-4xm\left(3\sqrt{x}-2\right)>\left(\sqrt{x}+2\right)\cdot\left(x+1\right)\)
=>\(-12m\cdot x\sqrt{x}+8xm>x\sqrt{x}+2x+\sqrt{x}+2\)
=>\(x\sqrt{x}\left(-12m-1\right)+x\left(8m-2\right)-\sqrt{x}-2>0\)
Để BPT luôn đúng thì m<-0,3