BL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AT
19 tháng 7 2021
a) \(5\sqrt{25a^2}-25=25\left|a\right|-25==-25a-25\left(a< 0\right)\)
b) \(\sqrt{49a^2}+3a=7\left|a\right|+3a=-7a+3a\left(a< 0\right)=-4a\)
c) \(3\sqrt{9a^6}=9\left|a^3\right|-6a^3\)
Xét \(a\ge0\Rightarrow9\left|a^3\right|-6a^3=9a^3-6a^3=3a^3\)
Xét \(a< 0\Rightarrow9\left|a^3\right|-6a^3=-9a^3-6a^3=-15a^3\)
19 tháng 7 2021
a) 5\(\sqrt{25a^2}\) - 25 với a < 0
= 5\(\sqrt{\left(5a\right)^2}\) - 25
= 5.\(\left|5a\right|\) - 25
= 5.-(5a) - 25
= -25a - 25 Vì a < 0
b) \(\sqrt{49a^2}\) + 3a với a < 0
= \(\sqrt{\left(7a\right)^2}\) + 3a
= \(\left|7a\right|\) + 3a
= -7a + 3a Vì a < 0
= -4a
c) 3\(\sqrt{9a^6}\) - 6a3 với a bất kì
= 3\(\sqrt{\left(3a^3\right)^2}\) - 6a3
= 3\(\left|3a^3\right|\) - 6a3
= 9a3 - 6a3
= 3a3
Chúc bạn học tốt
5 tháng 6 2021
`A=sqrt{1+1/a^2+1/(a+1)^2}`
`=sqrt{1/a^2+2/a+1-2/a+1/(a+1)^2}`
`=sqrt{(1/a+1)^2-2/a+1/(a+1)^2}`
`=sqrt{(a+1)^2/a^2-2.(a+1)/a.(1/(a+1))+1/(a+1)^2}`
`=sqrt{((a+1)/a-1/(a+1))^2}`
`=|(a+1)/a-1/(a+1)|`
`=|1+1/a-1/(a+1)|`
`a>0=>1/a>1/(a+1)=>1+1/a-1/(a+1)>0`
`=>A=1+1/a-1/(a+1)`
5 tháng 6 2021
Áp dụng công thức ở A ta tính được
`B=1+1/1-1/2+1+1/2-1/3+1-1/3+1/4+.......+1+1/(n-1)-1/n`(ở sau bạn không ghi rõ nên mình đặt số cuối là n)
`=underbrace{1+1+....+1}_{\text{n chữ số 1}}-1/n`
`=n-1/n`
8 tháng 11 2021
a) \(=5\left|a\right|+3a=5a+3a=8a\)
b) \(=3\left|a^2\right|+3a^2=3a^2+3a^2=6a^2\)
c) \(=5.2\left|a^3\right|-3a^3=-10a^3-3a^3=-13a^3\)
CM
17 tháng 11 2019
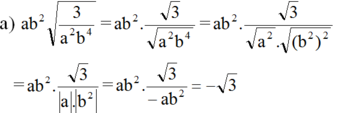
(vì a < 0 nên |a| = -a, b2 > 0 với mọi b ≠ 0 nên |b2| = b2 )
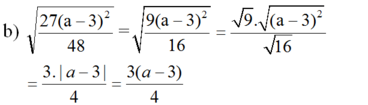
(vì a > 3 nên |a - 3| = a - 3)
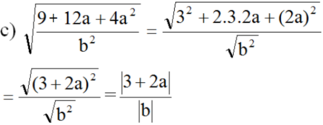
Vì b < 0 nên |b| = -b
Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a
Vậy:
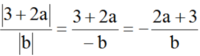
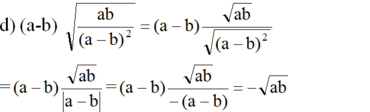
(vì a < b < 0 và b < 0 nên |a - b| = -(a - b), ab > 0)
28 tháng 6 2021
-Chia nhỏ ra bạn ơi để nhận được câu tl sớm nhất.
-Bạn đặt không mất gì nên cứ đặt thoải mái đuyyy.
-Để dài như này khum ai làm đouuu.
28 tháng 6 2021
a) Ta có: \(A=\left(\dfrac{1}{\sqrt{x}-3}+\dfrac{1}{x-3\sqrt{x}}\right):\dfrac{2}{\sqrt{x}-3}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{2}\)
\(=\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)
b) Thay \(x=3-2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{\sqrt{2}-1+1}{2\cdot\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{2}}{2\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{2}=\dfrac{2+\sqrt{2}}{2}\)
c) Để \(A< \dfrac{2}{3}\) thì \(\dfrac{\sqrt{x}+1}{2\sqrt{x}}-\dfrac{2}{3}< 0\)
\(\Leftrightarrow\dfrac{3\left(\sqrt{x}+1\right)-4\sqrt{x}}{6\sqrt{x}}< 0\)
\(\Leftrightarrow-\sqrt{x}+3< 0\)
\(\Leftrightarrow-\sqrt{x}< -3\)
\(\Leftrightarrow\sqrt{x}>3\)
hay x>9
Vậy: Để \(A< \dfrac{2}{3}\) thì x>9
a) \(\sqrt{0,49\cdot a^2}=\sqrt{0,7^2\cdot a^2}=\sqrt{\left(0,7\cdot\left|a\right|\right)^2}=0,7\left|a\right|\) (với a < 0)
b) \(\sqrt{25\left(7-a\right)^2}=\sqrt{\left[5\left(7-a\right)\right]^2}=5\left|7-a\right|\) (với a >/ 7)
c) \(\sqrt{a^4\left(a-2\right)^2}=a^2\left(a-2\right)=a^3-2a\) (với a >0 )
Tớ mới học nên cx ko chắc chắn lắm nhé.