
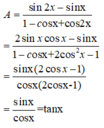
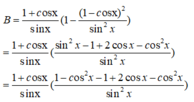
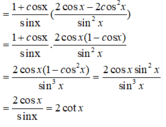
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

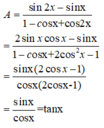
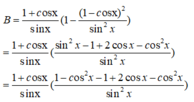
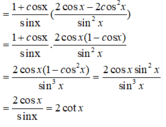

a, \(\left(1-sin^2x\right)cot^2x+1-cot^2x\)
\(=cot^2x-sin^2x.cot^2x+1-cot^2x\)
\(=1-sin^2x.\frac{\text{cos}^2x}{sin^2x}=1-\text{cos}^2x=sin^2x\)
b,\(\left(tanx+cotx\right)^2-\left(tanx-cotx\right)2\)
\(=tan^2x2.tanx.cotx+cot^2x-tan^2x+2tanx.cotx-cot^2x\)
\(=4tanxcotx=4\)
c,\(\left(xsina-y\text{cos}a\right)^2+\left(x\text{cos}a+ysina\right)^2\)
\(=x^2sin^2a=2xysina\text{cos}a+y^2\text{cos}^2a+2xysina\text{cos}a+y^2sin^2a\)
\(=x^2\left(sin^2a+\text{cos}^2a\right)+y^2\left(sin^2a+\text{cos}^2a\right)\)
\(=x^2+y^2\)

Lời giải:
a)
\(\frac{1-\cos x}{\sin x}=\frac{(1-\cos x)(1+\cos x)}{\sin x(1+\cos x)}=\frac{1-\cos ^2x}{\sin x(1+\cos x)}=\frac{\sin ^2x}{\sin x(1+\cos x)}=\frac{\sin x}{1+\cos x}\)
b)
\((\sin x+\cos x-1)(\sin x+\cos x+1)=(\sin x+\cos x)^2-1^2\)
\(=\sin ^2x+\cos ^2x+2\sin x\cos x-1=1+2\sin x\cos x-1=2\sin x\cos x\)
c)
\(\frac{\sin ^2x+2\cos x-1}{2+\cos x-\cos ^2x}=\frac{1-\cos ^2x+2\cos x-1}{2+\cos x-\cos ^2x}=\frac{-\cos ^2x+2\cos x}{2+\cos x-\cos ^2x}\)
\(=\frac{\cos x(2-\cos x)}{(2-\cos x)(\cos x+1)}=\frac{\cos x}{\cos x+1}\)
d)
\(\frac{\cos ^2x-\sin ^2x}{\cot ^2x-\tan ^2x}=\frac{\cos ^2x-\sin ^2x}{\frac{\cos ^2x}{\sin ^2x}-\frac{\sin ^2x}{\cos ^2x}}=\frac{\sin ^2x\cos ^2x(\cos ^2x-\sin ^2x)}{\cos ^4x-\sin ^4x}\)
\(=\frac{\sin ^2x\cos ^2x(\cos ^2x-\sin ^2x)}{(\cos ^2x-\sin ^2x)(\cos ^2x+\sin ^2x)}=\frac{\sin ^2x\cos ^2x}{\sin ^2x+\cos ^2x}=\sin ^2x\cos ^2x\)
e)
\(1-\cot ^4x=1-\frac{\cos ^4x}{\sin ^4x}=\frac{\sin ^4x-\cos ^4x}{\sin ^4x}=\frac{(\sin ^2x-\cos ^2x)(\sin ^2x+\cos ^2x)}{\sin ^4x}\)
\(=\frac{\sin ^2x-\cos ^2x}{\sin ^4x}=\frac{\sin ^2x-(1-\sin ^2x)}{\sin ^4x}=\frac{2\sin ^2x-1}{\sin ^4x}=\frac{2}{\sin ^2x}-\frac{1}{\sin ^4x}\)
Ta có ddpcm.

Bạn kiểm tra lại đề bài câu 1, câu này chỉ có thể rút gọn đến \(2cot^2x+2cotx+1\) nên biểu thức ko hợp lý
Đồng thời kiểm tra luôn đề câu 2, trong cả 2 căn thức đều xuất hiện \(6sin^2x\) rất không hợp lý, chắc chắn phải có 1 cái là \(6cos^2x\)

\(sinx+cosx=m\Leftrightarrow\left(sinx+cosx\right)^2=m^2\)
\(\Leftrightarrow1+2sinx.cosx=m^2\Rightarrow sinx.cosx=\dfrac{m^2-1}{2}\)
\(A=sin^2x+cos^2x=1\)
\(B=sin^3x+cos^3x=\left(sinx+cosx\right)^3-3sinx.cosx\left(sinx+cosx\right)\)
\(=m^3-\dfrac{3m\left(m^2-1\right)}{2}=\dfrac{2m^3-3m^3+3m}{2}=\dfrac{3m-m^3}{2}\)
\(C=\left(sin^2+cos^2x\right)^2-2\left(sinx.cosx\right)^2=1-2\left(\dfrac{m^2-1}{2}\right)^2\)
\(D=\left(sin^2x\right)^3+\left(cos^2x\right)^3=\left(sin^2x+cos^2x\right)^3-3\left(sin^2x+cos^2x\right)\left(sinx.cosx\right)^2\)
\(=1-3\left(\dfrac{m^2-1}{2}\right)^2\)

\(a)sin^4x+cos^4x=1-2sin^2x\cdot cos^2x\)
\(\Leftrightarrow sin^4x+2sin^2x\cdot cos^2x+cos^4x=1\)
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2=1\)(luôn đúng)

a) Ta có: \(1-\frac{\sin^2x}{1+\cot x}-\frac{\cos^2x}{1+\tan x}=1-\frac{\sin^2x}{1+\frac{\cos x}{\sin x}}-\frac{\cos^2x}{1+\frac{\sin x}{\cos x}}\) (Đk: sinx và cosx khác 0)
\(=1-\frac{\sin^3x}{\sin x+\cos x}-\frac{\cos^3x}{\cos x+\sin x}\)
\(=1-\frac{\left(\sin x+\cos x\right)\left(\sin^2x-\sin x.\cos x+\cos^2x\right)}{\sin x+\cos x}\)
\(=1-\left(\sin^2x+\cos^2x-\sin x.\cos x\right)\) (do sinx + cosx luôn khác 0)
\(=\sin x.\cos x\) ( do \(\sin^2x+\cos^2x=1\))
b) Ta có: \(\frac{\sin^2x+2\cos x-1}{2+\cos x-\cos^2x}=\frac{\left(\sin^2x-1\right)+2\cos x}{-\left(\cos x+1\right)\left(\cos x-2\right)}\) (Đk: cosx khác -1 và 2)
\(=\frac{-\cos x\left(\cos x-2\right)}{-\left(\cos x+1\right)\left(\cos x-2\right)}\)
\(=\frac{\cos x}{1+\cos x}\)
a) Ta có: 1−sin2x1+cotx −cos2x1+tanx =1−sin2x1+cosxsinx −cos2x1+sinxcosx (Đk: sinx và cosx khác 0)
=1−sin3xsinx+cosx −cos3xcosx+sinx
=1−(sinx+cosx)(sin2x−sinx.cosx+cos2x)sinx+cosx
=1−(sin2x+cos2x−sinx.cosx) (do sinx + cosx luôn khác 0)
=sinx.cosx ( do sin2x+cos2x=1)
b) Ta có: sin2x+2cosx−12+cosx−cos2x =(sin2x−1)+2cosx−(cosx+1)(cosx−2) (Đk: cosx khác -1 và 2)
=−cosx(cosx−2)−(cosx+1)(cosx−2)
=cosx1+cosx

1234567890-01234567890-=qưertyuiop[]\';;lkjhfgdsazxcvbnm,./\'l;[]7894561230.+-

\(\frac{sinx+cosx-1}{sinx-cosx+1}=\frac{\left(sinx+cosx-1\right)\left(sinx-\left(cosx-1\right)\right)}{\left(sinx-cosx+1\right)^2}\)
\(=\frac{sin^2x-\left(cosx-1\right)^2}{sin^2x+cos^2x+1-2sinx.cosx+2sinx-2cosx}=\frac{sin^2x-cos^2x+2cosx-1}{2\left(1-cosx+sinx-sinx.cosx\right)}\)
\(=\frac{1-cos^2x-cos^2x+2cosx-1}{2\left(1-cosx\right)\left(1+sinx\right)}=\frac{cosx\left(1-cosx\right)}{\left(1-cosx\right)\left(1+sinx\right)}=\frac{cosx}{1+sinx}\)

a) \(\left(sinx+cosx\right)^2=sin^2x+2sinxcosx+cos^2x\)\(=1+2sinxcosx\).
b) \(\left(sinx-cosx\right)^2=sin^2x-2sinxcosx+cos^2x\)\(=1-2sinxcosx\).
c) \(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\).