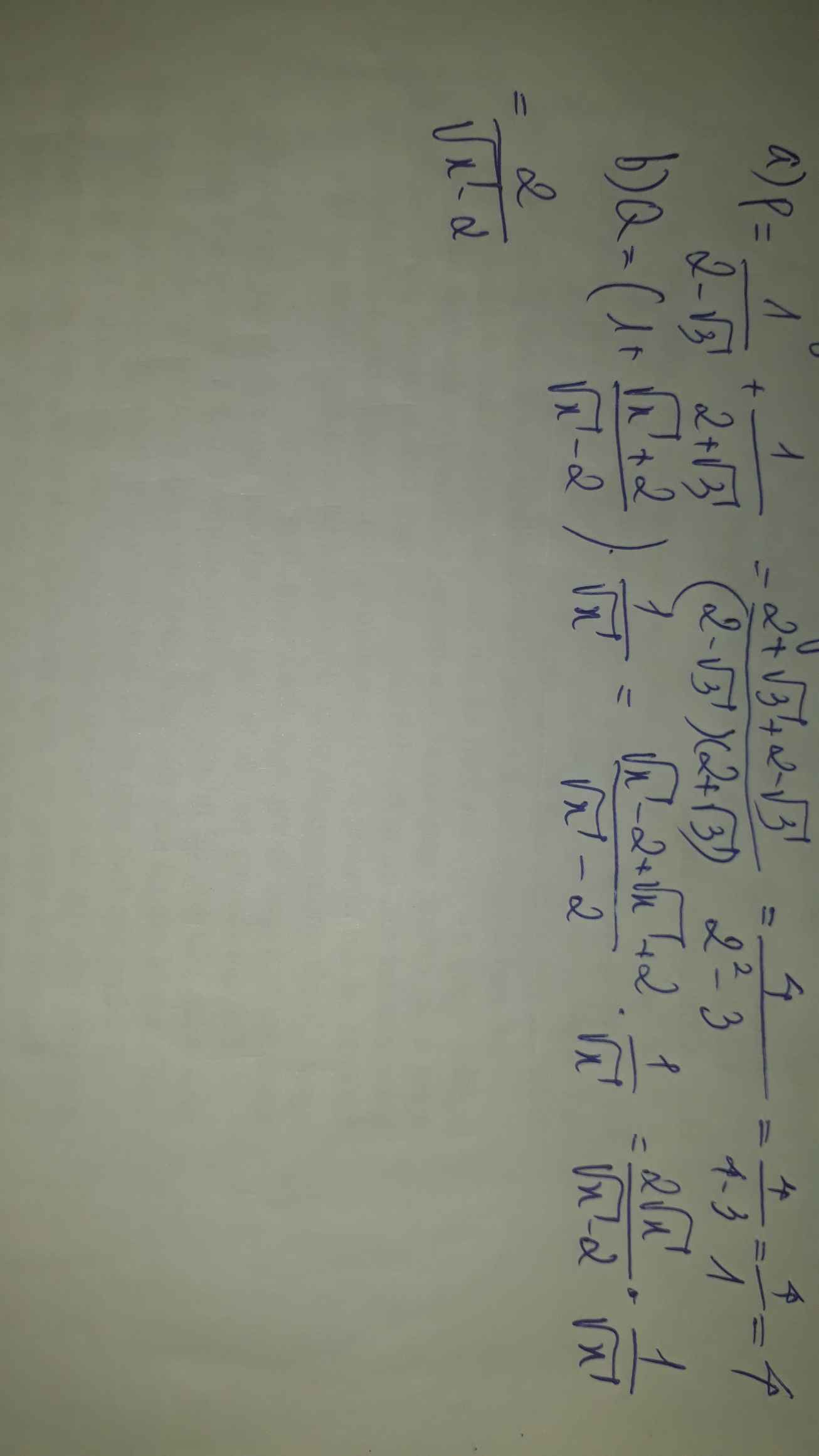Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x+1}{x-1}\) \(\left(\text{Đ}K:x\ge0;x\ne1\right)\)
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+\sqrt{x}+1}{x-1}\right).\dfrac{x-1}{x+1}\)
\(=\dfrac{x+1}{x+1}=1\)

1, vt : \(\left(1-\dfrac{5+\sqrt{2}}{\sqrt{2}+1}\right).\sqrt{3+2\sqrt{2}}\)
=\(\dfrac{\sqrt{2}+1-5-\sqrt{2}}{\sqrt{2}+1}.\sqrt{\left(\sqrt{2}\right)^2+2\sqrt{2}+1}\)
=\(\dfrac{-4}{\sqrt{2}+1}.\sqrt{\left(\sqrt{2}+1\right)^2}\)
=\(\dfrac{-4\left(\sqrt{2}+1\right)}{\sqrt{2}+1}\)
=-4
2, A=\(\left(\dfrac{\sqrt{x}}{x+\sqrt{x}}-\dfrac{1}{\sqrt{x}-1}\right)\div\dfrac{2}{x+\sqrt{x}-2}\)
=\(\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right).\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{2}\)
=\(\left(\dfrac{x-\sqrt{x}-x-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{2}\)
=\(\dfrac{-2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{2}\)
=\(\dfrac{-\sqrt{x}-2}{\sqrt{x}+1}\)

a) \(P=\dfrac{1}{2-\sqrt{3}}+\dfrac{1}{2+\sqrt{3}}\)
\(=\dfrac{2+\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}+\dfrac{2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\dfrac{2+\sqrt{3}+2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\dfrac{4}{4-3}\)
\(=4\)
b) \(Q=\left(1+\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\right).\dfrac{1}{\sqrt{x}}vớix>0,x\ne4\)
\(=\left(\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\sqrt{x}-2}\right).\dfrac{1}{\sqrt{x}}\)
\(=\)\(\dfrac{2\sqrt{x}}{\sqrt{x}-2}.\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2}{\sqrt{x}-2}\)

1. \(x=\frac{1}{9}\) thỏa mãn đk: \(x\ge0;x\ne9\)
Thay \(x=\frac{1}{9}\) vào A ta có:
\(A=\frac{\sqrt{\frac{1}{9}}+1}{\sqrt{\frac{1}{9}}-3}=-\frac{1}{2}\)
2. \(B=...\)
\(B=\frac{3\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\frac{4x+6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{3x-9\sqrt{x}+x+3\sqrt{x}-4x-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
3. \(P=A:B=\frac{\sqrt{x}+1}{\sqrt{x}-3}:\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\frac{\sqrt{x}+3}{-6}\)
Vì \(\sqrt{x}+3\ge3\forall x\)\(\Rightarrow\frac{\sqrt{x}+3}{-6}\le\frac{3}{-6}=-\frac{1}{2}\)
hay \(P\le-\frac{1}{2}\)
Dấu "=" xảy ra <=> x=0

x2-4x-5=0
⇔x2-5x+x-5=0
⇔(x2+x)-(5x+5)=0
⇔x(x+1)-5(x+1)=0
⇔(x-5)(x+1)=0
⇔\(\left\{{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
vậy phương trình có 2 nghiệm phân biệt x=5;x=-1
b, A=\(\dfrac{x}{x-4}\)+\(\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)
=\(\dfrac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{2\sqrt{x}+x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{\sqrt{x}\left(2+\sqrt{x}\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)}\)

a) Ta có: \(A=\left(\dfrac{1}{\sqrt{a}+2}+\dfrac{1}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}}{a-4}\)
\(=\dfrac{\sqrt{a}-2+\sqrt{a}+2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\cdot\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\sqrt{a}}\)
=2
b) Ta có: \(B=\left(\dfrac{4x}{\sqrt{x}-1}-\dfrac{\sqrt{x}-2}{x-3\sqrt{x}+2}\right)\cdot\dfrac{\sqrt{x}-1}{x^2}\)
\(=\dfrac{4x-1}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}-1}{x^2}\)
\(=\dfrac{4x-1}{x^2}\)