ND
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HS
25 tháng 8 2018
\(a,\sqrt{64a^2}+2a\left(a\ge0\right)\\ < =>\sqrt{8^2.a^2}+2a\\ < =>\sqrt{\left(8a\right)^2+2a}\\ < =>\left|8a\right|+2a\\ < =>8a+2a\\ < =>10a\left(TM\right)vìa\ge0\)
\(b,3\sqrt{9a^6}-6a^3\left(a\in R\right)\\ < =>3\sqrt{\left(3a^2\right)^2}-6a^3\\ < =>3\left|3a^3\right|-6a^3\\ \)
Nếu \(a\ge0\) thì giá trị của biểu thức là:
\(3.3a^2-6a^2\\ =9a^3-6a^3\\ =3a^3\)
Nếu a<0 thì giá trị của biểu thức là:
\(3\left(-3a^3\right)-6a^3=-9a^3\\ =-6a^3=-15a^3\)
\(c,\sqrt{a^2+6a+9}+\sqrt{a^2-6a+9}\left(a\ge3\right)\\ =\sqrt{\left(a+3\right)^2}+\sqrt{\left(a-3\right)^2}\\ =\left|a+3\right|+\left|a-3\right|\\ =a+3+a-3\\ =2a\)
HV
Rút gọn biểu thức
A=Căn ((2 căn 10 + căn 30 - 2 căn 2 - căn 6)/(2 căn 10 - 2 căn 2)) ÷ 2/ ( căn 3 -1)
0
AH
Akai Haruma
Giáo viên
10 tháng 6 2021
Bạn vui lòng viết đề bằng công thức toán để được hỗ trợ tốt hơn.
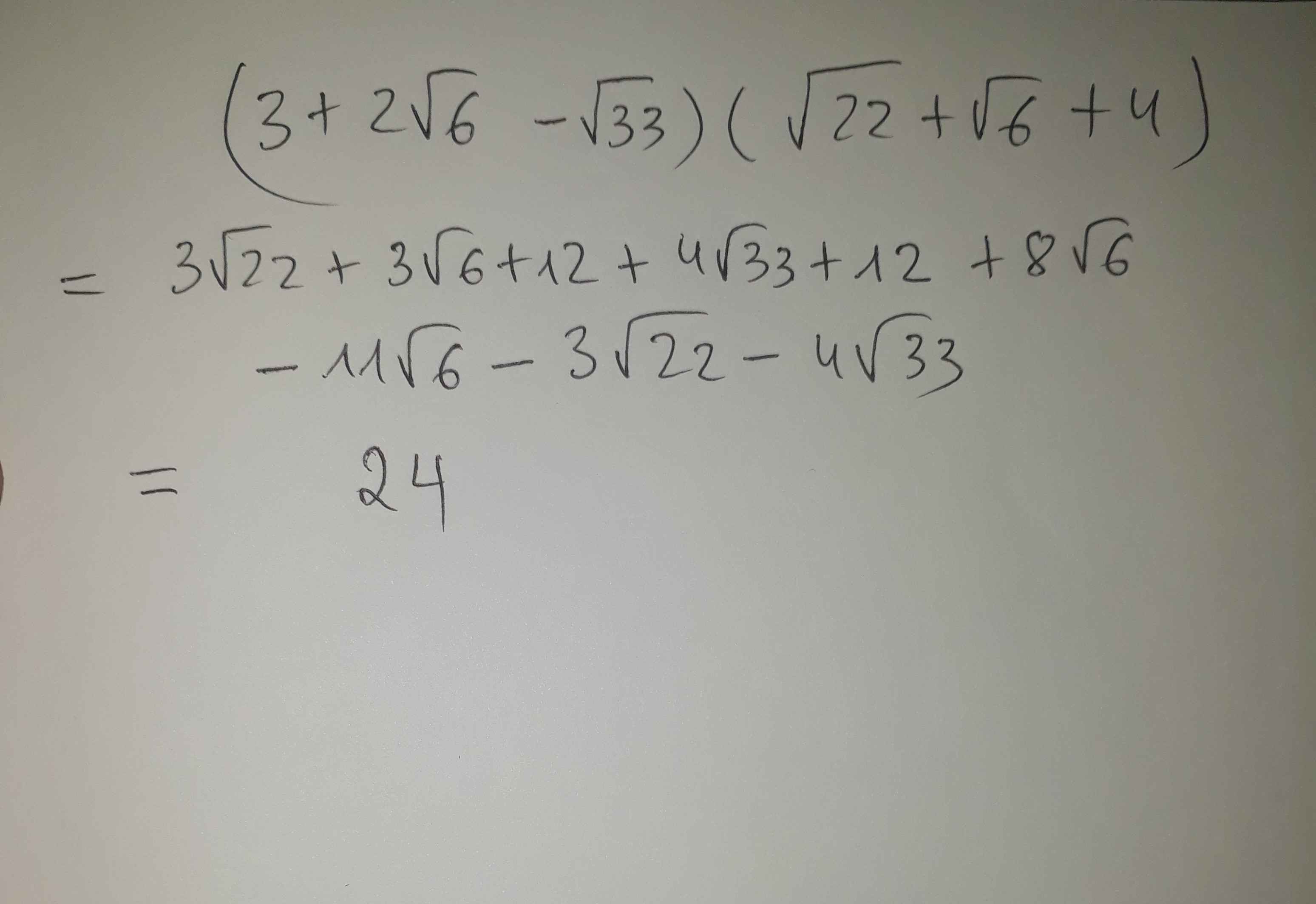
\(A=\sqrt{64a^2}\cdot2a=\sqrt{\left(8a\right)^2}\cdot2a=\left|8a\right|\cdot2a\)
Với a < 0 A = 8a.(-2a) = -16a2
Với a ≥ 0 A = 8a.2a = 16a2
\(B=3\sqrt{9a^6}-6a^3=3\sqrt{\left(3a^3\right)^2}-6a^3=9\left|a^3\right|-6a^3\)