N
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 6 2021
`c)root{3}{4}.root{3}{1-sqrt3}.root{6}{(sqrt3+1)^2}`
`=root{3}{4(1-sqrt3)}.root{3}{1+sqrt3}`
`=root{3}{4(1-sqrt3)(1+sqrt3)}`
`=root{3}{4(1-3)}=-2`
`d)2/(root{3}{3}-1)-4/(root{9}-root{3}{3}+1)`
`=(2(root{3}{9}+root{3}{3}+1))/(3-1)-(4(root{3}{3}+1))/(3+1)`
`=root{3}{9}+root{3}{3}+1-root{3}{3}-1`
`=root{3}{9}`
24 tháng 6 2021
`a)root{3}{8sqrt5-16}.root{3}{8sqrt5+16}`
`=root{3}{(8sqrt5-16)(8sqrt5+16)}`
`=root{3}{320-256}`
`=root{3}{64}=4`
`b)root{3}{7-5sqrt2}-root{6}{8}`
`=root{3}{1-3.sqrt{2}+3.2.1-2sqrt2}-root{6}{(2)^3}`
`=root{3}{(1-sqrt2)^3}-sqrt2`
`=1-sqrt2-sqrt2=1-2sqrt2`
NN
1
KN
24 tháng 6 2019
b) \(\sqrt{\left(7-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{3}+1\right)^2}\)
\(=7-\sqrt{3}+\sqrt{3}+1\)
\(=8\)
11 tháng 11 2021
Bài 1:
\(a,ĐK:2+8x\ge0\Leftrightarrow x\ge-\dfrac{1}{4}\\ b,ĐK:-\dfrac{1}{5}x+9\ge0\Leftrightarrow-\dfrac{1}{5}x\ge-9\Leftrightarrow x\le45\\ c,ĐK:11-7x\ge0\Leftrightarrow x\le\dfrac{11}{7}\)
Bài 2:
\(a,=\sqrt{144a^2}-2a=12\left|a\right|-2a=12a-2a=10\\ b,=\sqrt{6}-6\sqrt{6}-\sqrt{6}=-6\sqrt{6}\)
Bài 3:
\(a,\Leftrightarrow\left|2x+3\right|=3\Leftrightarrow\left[{}\begin{matrix}2x+3=3\\2x+3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\\ b,ĐK:x\ge2\\ PT\Leftrightarrow2\sqrt{x-2}-4\sqrt{x-2}+3\sqrt{x-2}=4\\ \Leftrightarrow\sqrt{x-2}=4\\ \Leftrightarrow x-2=16\\ \Leftrightarrow x=18\left(tm\right)\)
VL
4
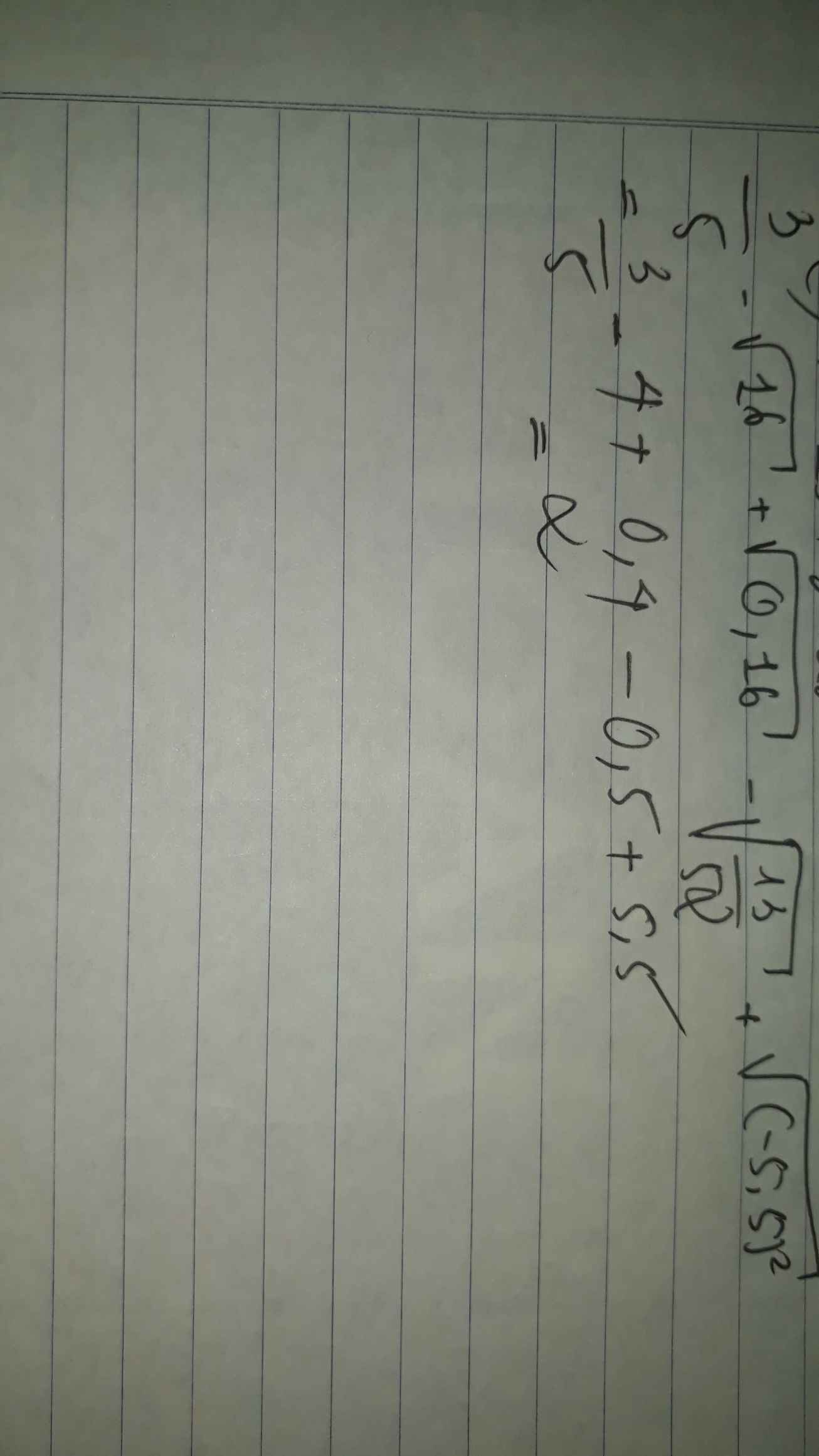
\(5\sqrt[3]{2}+\sqrt[3]{-16}+\sqrt[3]{54}=5\sqrt[3]{2}-2\sqrt[3]{2}+3\sqrt[3]{2}=6\sqrt[3]{2}\)
\(5\sqrt[3]{2}+\sqrt[3]{-16}+\sqrt[3]{54}\)
\(=5\sqrt[3]{2}-2\sqrt[3]{2}+3\sqrt[3]{2}\)
\(=6\sqrt[3]{2}\)