Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có đầy câu hỏi tương tự đáy bạn lên các câu hỏi đó mà xem

a: \(A=\dfrac{a^3+a^2+a^2+a-a-1}{\left(a+1\right)\left(a^2-a+1\right)+2a\left(a+1\right)}\)
\(=\dfrac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2+a+1\right)}=\dfrac{a^2+a-1}{a^2+a+1}\)
b: Nếu a là số nguyên âm thì a<0
Vì a2+a=a(a+1) chia hết cho 2 nên \(a^2+a-1;a^2+a+1\) là hai số tự nhiên lẻ liên tiếp
hay A là phân số tối giản

a) A=x^2+2
b) mình nghĩ x thuộc tập hợp R
c)GTNN của A=1/4 khi x=1/2

a) Ta có:
\(A=\left(a-4\right)\left(a+5\right)-\left(a-5\right)\left(a+4\right)\)
\(=\left[\left(a-4\right)a+5\left(a-4\right)\right]-\left[\left(a-5\right)a+4\left(a-5\right)\right]\)
\(=\left[a^2-4a+5a-20\right]-\left[a^2-5a+4a-20\right]\)
\(=a^2-4a+5a-20-a^2+5a-4a+20\)
\(=\left(a^2-a^2\right)+\left(-4a+5a+5a-4a\right)+\left(-20+20\right)\)
\(=0+2a+0\)
\(=2a\)
b) Ta có:
\(B=\left(2-a\right)\left(a+7\right)-\left(a-1\right)\left(a+2\right)\)
\(=\left[\left(2-a\right)a+7\left(2-a\right)\right]-\left[\left(a-1\right)a+2\left(a-1\right)\right]\)
\(=\left[2a-a^2+14-7a\right]-\left[a^2-a+2a-2\right]\)
\(=2a-a^2+14-7a-a^2+a-2a+2\)
\(=\left(2a-7a+a-2a\right)-\left(a^2+a^2\right)+\left(14+2\right)\)
\(=-6a-2a^2+16\)

Lời giải:
Từ điều kiện đề bài dễ dàng suy ra \(a,b,c<\sqrt{3}<2\)
Sử dụng phương pháp hệ số bất định, ta sẽ CM: \(2a+\frac{1}{a}\geq \frac{5}{2}+\frac{a^2}{2}\)
BĐT này luôn đúng vì \(\Leftrightarrow (2-a)(a-1)^2\geq 0\)
Thiết lập tương tự với $b,c$, suy ra \(2(a+b+c)+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{15}{2}+\frac{a^2+b^2+c^2}{2}=9\) (đpcm)
Dấu $=$ xảy ra khi $a=b=c=1$

Có ABCD là hình bình hành nên A D ⇀ = B C ⇀ = - 1 ; 3 ; 7 ⇒ D 0 ; 5 ; 10
Chọn đáp án C.

Câu 1 :
Đk: \(x\ge1\)
\(\sqrt{x-1}+\sqrt{2x-1}=5\\ \Leftrightarrow x-1+2\sqrt{\left(x-1\right)\left(2x-1\right)}+2x-1=25\\ \Leftrightarrow2\sqrt{2x^2-3x+1}=27-3x\\ \)
\(\Leftrightarrow\begin{cases}27-3x\ge0\\4\left(2x^2-3x+1\right)=9x^2-162x+729\end{cases}\) \(\Leftrightarrow\begin{cases}x\le9\\x^2-150x+725=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x\le9\\x=145hoặcx=5\end{cases}\)
với x= 5 thoản mãn điều kiện, x=145 loại
Vậy \(S=\left\{5\right\}\)
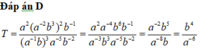
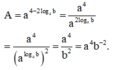
Chọn C