Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Các mặt: ABCD, A’B’C’D’, ABB’A’, CDD’C’, ADD’A’, BCC’B’
- BB’ và AA’ có cùng nằm trong một mặt phẳng là ABB’A’
- BB’ và AA’ không có điểm chung

- AB có song song với A’B’ vì là hai cạnh đối nhau của hình chữ nhật ABB’A’
- AB không nằm trong mặt phẳng (A’B’C’D’)

- AB có song song với A’B’ vì là hai cạnh đối nhau của hình chữ nhật ABB’A’
- AB không nằm trong mặt phẳng (A’B’C’D’)

- Các mặt: ABCD, A'B'C'D', ABB'A', CDD'C', ADD'A', BCC'B'
- Các đỉnh: A, B, C, D, A', B', C', D'
- Các cạnh: AB, BC, CD, DA, A'B', B'C', C'D', D'A', AA', BB', CC', DD'

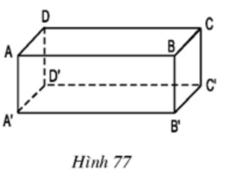
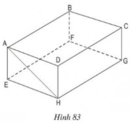
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

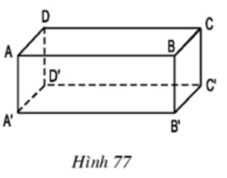
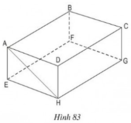
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

a: \(mp\left(EFGH\right);mp\left(ABCD\right)\)
\(mp\left(ABFE\right);mp\left(CDHG\right)\)
\(mp\left(ADHE\right);mp\left(BCGF\right)\)
b: Các điểm D,H,G,C cùng thuộc mặt phẳng CDHG
c: Các điểm D,H,G,F không thuộc cùng một mặt phẳng
d: A,B,G,H cùng thuộc mặt phẳng ABGH
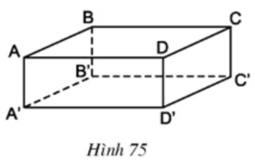
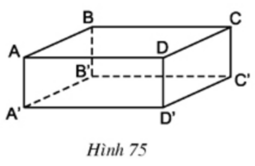
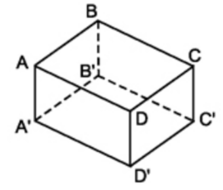

- Các mặt: (ABCD), (A’B’C’D’), (ABB’A’), (CDD’C’), (ADD’A’), (BCC’B’)
- BB’ và AA’ có cùng nằm trong một mặt phẳng là (ABB’A’)
- BB’ và AA’ không có điểm chung