Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những cặp mặt phẳng song song với nhau là:
mp(ABCD) và mp(XYHK)
mp(ADKX) và mp(BCHY)
mp(ABYX) và mp(CDKH)

a: \(mp\left(EFGH\right);mp\left(ABCD\right)\)
\(mp\left(ABFE\right);mp\left(CDHG\right)\)
\(mp\left(ADHE\right);mp\left(BCGF\right)\)
b: Các điểm D,H,G,C cùng thuộc mặt phẳng CDHG
c: Các điểm D,H,G,F không thuộc cùng một mặt phẳng
d: A,B,G,H cùng thuộc mặt phẳng ABGH

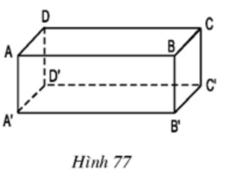
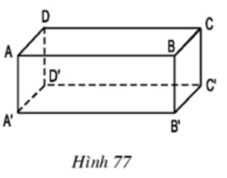
- AB có song song với A’B’ vì là hai cạnh đối nhau của hình chữ nhật ABB’A’
- AB không nằm trong mặt phẳng (A’B’C’D’)

- AB có song song với A’B’ vì là hai cạnh đối nhau của hình chữ nhật ABB’A’
- AB không nằm trong mặt phẳng (A’B’C’D’)

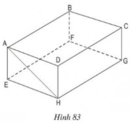
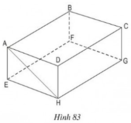
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

c) Mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).
a) Ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD.
b) Cạnh CD song song với hai mặt phẳng (ABEF) và (EFGH).
c) Mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

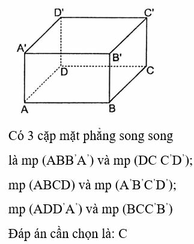

Các cặp mặt phẳng song song với nhau:
mp(EFGH) và mp(ABCG)
mp(ABFE) và mp(CDHG)
mp(ADHE) và mp(BCGF)