Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có hai trường hợp:
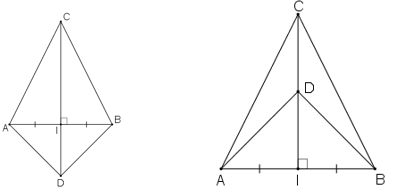
+ ΔAIC = ΔBIC (c.g.c) vì:
AI = IB (gt)
∠AIC = ∠BIC = 90o
CI chung.
+ ΔAID = ΔBID(c.g.c) vì:
AI = ID (gt)
∠AID = ∠BID = 90o
DI chung.
+ ΔACD = ΔBCD(c.c.c) vì:
AC = BC (Lấy từ ΔAIC = ΔBIC)
AD = BD (Lấy từ ΔAID = ΔBID)
CD chung

Xét tam giác ACI và tam giác BCI , có
CI là cạnh chung
AC = BC
AI= BI
=> tam giác ACI = tam giác BCI
Xét tam giác ACD và tam giác BCD , có
CD là cạnh chung
AD = BD
AC =BC
=> tam giác ACD = tam giác BCD
Xét tam giác ADI và tam giác BDI , có
DI là cạnh chung
AD = BD
AI = BI
=> tam giác ADI = tam giác BDI
ok 3 cặp nha
Vì ID là tia phân giác của đoạn thẳng AB
=> AD = BD
AI = BI
Xét ∆ AID và ∆ BID có :
AD = BD ( cmt )
ID là cạnh chung
AI = BI ( cmt )
=> ∆ AID = ∆ BID ( c.c.c )
Xét ∆ ACI và ∆ IBC có :
AC = BC ( theo hình vẽ )
IC là cạnh chung
AI = BI ( cmt )
=> ∆ ACI = ∆ IBC ( c.c.c )
Xét ∆ ACD và ∆ BCD có :
AD = BD ( cmt )
CD là cạnh chung
AC = BC ( cmt )
=> ∆ ACD = ∆ BCD ( c.c.c )
Vậy có 3 cặp tam giác bằng nhau
Cũng có thể chứng minh theo cách cạnh - góc - cạnh nhưng mình thích cạnh - cạnh - cạnh hơn :3

Xét tam giác ACI và tam giác BCI , có
CI là cạnh chung
AC = BC
AI= BI
=> tam giác ACI = tam giác BCI
Xét tam giác ACD và tam giác BCD , có
CD là cạnh chung
AD = BD
AC =BC
=> tam giác ACD = tam giác BCD
Xét tam giác ADI và tam giác BDI , có
DI là cạnh chung
AD = BD
AI = BI
=> tam giác ADI = tam giác BDI
ok 3 cặp nha thư
Có hai trường hợp:
+ ΔAIC = ΔBIC (c.g.c) vì:
AI = IB (gt)
∠AIC = ∠BIC = 90o
CI chung.
+ ΔAID = ΔBID(c.g.c) vì:
AI = ID (gt)
∠AID = ∠BID = 90o
DI chung.
+ ΔACD = ΔBCD(c.c.c) vì:
AC = BC (Lấy từ ΔAIC = ΔBIC)
AD = BD (Lấy từ ΔAID = ΔBID)
CD chung

b: Xét ΔCIA vuông tại I và ΔCIB vuông tại I có
CI chung
IA=IB
Do đó: ΔCIA=ΔCIB
Suy ra: \(\widehat{ACI}=\widehat{BCI}\)
hay CI là tia phân giác của góc ACB

a) Xét ΔNAB có
I\(\in\)NI(gt)
M\(\in\)NB(gt)
IM//AB(gt)
Do đó: \(\dfrac{NI}{AI}=\dfrac{NM}{BM}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{NI}{AI}=1\)
\(\Leftrightarrow NI=AI\)
mà A,I,N thẳng hàng(gt)
nên I là trung điểm của AN(Đpcm)