Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)
\(\dfrac{B'B}{AB}=\dfrac{C'C}{AC}\)
\(\dfrac{AB'}{B'B}=\dfrac{AC'}{C'C}\)

https://diendan.hocmai.vn/threads/chung-minh-dinh-li-talet.287639/

vẽ hình(tự vẽ)
a) Xét △ABC có MN // BC(gt) ,theo định lí Ta-lét ta có:
\(\dfrac{AM}{MB}\)=\(\dfrac{AN}{NC}\) hay \(\dfrac{6}{4}\)=\(\dfrac{8}{NC}\)⇒NC=\(\dfrac{8.4}{6}\)=5,3(cm)
Ta có: AB=AM+BM=6+4=10(cm)
AC=AN+NC=8+5,3=13,3(cm)
Áp dụng định lý Py-ta-go vào △ABC vuông tại A ta có:
BC=\(\sqrt{AB^2+AC^2}\)=\(\sqrt{10^2+13,3^2}\)=\(\sqrt{276,89}\)=16,6(cm)
Xét △ABC có MN // BC,theo hệ quả định lí Ta -lét ta có:
\(\dfrac{AM}{AB}\)=\(\dfrac{MN}{BC}\)hay \(\dfrac{6}{10}\)=\(\dfrac{MN}{16,6}\)⇒MN=\(\dfrac{16,6.6}{10}\)=9,96(cm)
b)

Xét ΔODE và ΔOCB có
góc ODE=góc OCB
góc DOE=góc COB
=>ΔODE đồng dạng với ΔOCB
=>OD/OC=OE/OB
=>OD*OB=OC*OE

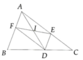
Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I
Định lí:
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.