Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: Độ phóng xạ H = H0.2-t/T
Cách giải:
H = 200; H0 = 1600
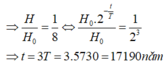
Đáp án D

Xét tỉ số giữa độ phóng xạ ở thời điểm \(t\) và độ phóng xạ ban đầu ( không cần chuyển đơn vị của độ phóng xạ từ phân rã / phút sang phân rã / giây vì dùng phép chia hai độ phóng xạ cho nhau.)
\(\frac{H}{H_0}= 2^{-\frac{t}{T}}= \frac{1}{8}= 2^{-3}.\)
=> \(t = 3T= 3.5730 = 17190 \)(năm).

Tỉ số giữa độ phóng xạ của tượng gỗ (sau thời gian t) so với độ phóng xạ của gỗ lúc mới chặt
\(\frac{H}{H_0}= 0,8= 2^{-\frac{t}{T}}\)
=> \(t = 0,32 T = 1802,8.( năm)\)
Như vậy tượng gỗ có gần 1803 năm tuổi.

Ho = 14 hạt/phút
Ht = 3 hạt/phútAD Ht=Ho.2−tTHt=Ho.2−tT=> t = 12378 năm
\(H=H_0\times2^{-\frac{t}{T}}\)
H0 là độ phóng xạ ban đầu ( có thể coi là độ phóng xạ của mẫu gỗ mới vì nó chưa phóng xạ)
H là độ phóng xạ sau khoảng thời gian t

1 hạt nhân \(_6^{14}C\) bị phân rã tạo thành 1 hạt nhân \(_7^{14}N\).
Tỉ số giữa số nguyên tử đã bị phóng xạ và số nguyên tử ban đầu là
\(\frac{\Delta N}{N_0}= 1-2^{-\frac{t}{T}}= 0,875.\)
=> \(2^{-\frac{t}{T}}= 0,125= 2^{-3}.\)
=> \(t = 3T = 16710\)(năm).
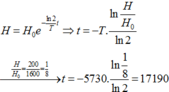
Độ phóng xạ của khúc gỗ mới chặt: \(H_0 = \lambda N_0\)
Độ phóng xạ của khúc gỗ cổ: \(H(t) = H'_{0}. 2^{-t/T} = \lambda. N'_{0} .2^{-t/T}\)
=> \(\frac{H_1}{H_2} = \frac{N_{0}}{N'_{0}} \frac{1}{2 ^ {t/T}} = 1,2.(1)\)
Lại có khối lượng của khúc gỗ cỗ lớn gấp đôi khối lượng của khúc gỗ mới chặt => \(m_0 ' = 2m_0 => \frac{N'_{0}}{N_0} = 2.(2)\)
Thay (2) vào (1) ta được: \(2 ^{t/T} = 2,4 => t = T \log_22,4 \approx 7072,9 \) năm.
Vậy tuổi của mẩu gỗ là: 7073 năm.
Chọn đáp án.C.7073 năm.