K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
a.
$64x^3-16x^2+x=x(64x^2-16x+1)$
$=x(8x-1)^2$
b.
$36-4xy+24y-x^2=(4y^2+24y+36)-(x^2+4xy+4y^2)$
$=(2y+6)^2-(x+2y)^2=(2y+6-x-2y)(2y+6+x+2y)$
$=(6-x)(x+4y+6)$
c.
$x^2+10x-2010.2020$
$=x^2+10x-(2015-5)(2015+5)
$=x^2+10x-(2015^2-5^2)$
$=(x^2+10x+5^2)-2015^2=(x+5)^2-2015^2$
$=(x+5-2015)(x+5+2015)=(x-2010)(x+2020)$
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
d.
$25x^2-121+22y-y^2$
$=(5x)^2-(y^2-22y+11^2)$
$=(5x)^2-(y-11)^2=(5x-y+11)(5x+y-11)$
e.
$(x^2+2x)(x^2+2x-2)-3$
$=(x^2+2x)^2-2(x^2+2x)-3$
$=(x^2+2x)^2+(x^2+2x)-3(x^2+2x)-3$
$=(x^2+2x)(x^2+2x+1)-3(x^2+2x+1)$
$=(x^2+2x+1)(x^2+2x-3)$
$=(x+1)^2[x(x-1)+3(x-1)]$
$=(x+1)(x-1)(x+3)$
31 tháng 7 2021
a) x3+4x-5 = x3-x2+x2+4x-5=(x3-x2)+(x2-x)+(5x-5)=x2(x-1)+x(x-1)+5(x-1)=(x2+x+5)(x-1)
b) x3-3x2+4=x3-2x2-x2+4=(x3-2x2)-(x2-4)=x2(x-2)-(x-2)(x+2)=(x2-x+2)(x-2)
c) x3+2x2+3x+2=x3+x2+x2+x+2x+2=(x3+x2)+(x2+x)+(2x+2)=x2(x+1)+x(x+1)+2(x+1)=(x2+x+2)(x+1)
d) bạn xem lại đề đúng ko
e) (x2+3x)2-2(x2+3x)-8=x4+6x3+9x2-2x2-6x-8=x4+6x3+7x2-6x-8=x4-x3+7x3-7x2+14x2-14x+8x-8=(x4-x3)+(7x3-7x2)+(14x2-14x)+(8x-8)=x3(x-1)+7x2(x-1)+14x(x-1)+8(x-1)=(x3+7x2+14x+8)(x-1)=(x3+x2+6x2+6x+8x+8)(x-1)=\(\left[\left(x^3+x^2\right)+\left(6x^2+6x\right)+\left(8x+8\right)\right]\left(x-1\right)\)\(=\left[x^2\left(x+1\right)+6x\left(x+1\right)+8\left(x+1\right)\right]\left(x-1\right)\)\(=\left(x^2+6x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left(x^2+2x+4x+8\right)\left(x+1\right)\left(x-1\right)\)\(=\left[\left(x^2+2x\right)+\left(4x+8\right)\right]\left(x+1\right)\left(x-1\right)\)\(=\left[x\left(x+2\right)+4\left(x+2\right)\right]\left(x+1\right)\left(x-1\right)\)=\(\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x+4\right)\)
f) (x2+4x+10)2-7(x2+4x+11)+7=(x2+4x+10)2-\(\left[7\left(x^2+4x+11\right)-7\right]\)\(=\left(x^2+4x+10\right)^2-7\left(x^2+4x+10\right)\)\(=\left(x^2+4x+10\right)\left(x^2+4x+3\right)\)
31 tháng 7 2021
a) Ta có: \(x^3+4x-5\)
\(=x^3-x+5x-5\)
\(=x\left(x-1\right)\left(x+1\right)+5\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x+5\right)\)
b) Ta có: \(x^3-3x^2+4\)
\(=x^3+x^2-4x^2+4\)
\(=x^2\left(x+1\right)-4\left(x-1\right)\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-4x+4\right)\)
\(=\left(x+1\right)\cdot\left(x-2\right)^2\)
c) Ta có: \(x^3+2x^2+3x+2\)
\(=x^3+x^2+x^2+x+2x+2\)
\(=x^2\left(x+1\right)+x\left(x+1\right)+2\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+x+2\right)\)
d) Ta có: \(x^2+2xy+y^2+2x+2y-3\)
\(=\left(x+y\right)^2+2\left(x+y\right)-3\)
\(=\left(x+y\right)^2+3\left(x+y\right)-\left(x+y\right)-3\)
\(=\left(x+y\right)\left(x+y+3\right)-\left(x+y+3\right)\)
\(=\left(x+y+3\right)\left(x+y-1\right)\)
CI
3
10 tháng 10 2021
a) \(xy^2-25x=x\left(y^2-25\right)=x\left(y-5\right)\left(y+5\right)\)
b) \(x\left(x-y\right)+2x-2y=x\left(x-y\right)+\left(2x-2y\right)=x\left(x-y\right)+2\left(x-y\right)=\left(x-y\right)\left(x+2\right)\)
c) \(x^3-3x^2-4x+12=\left(x^3-3x^2\right)-\left(4x-12\right)=x^2\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x^2-4\right)=\left(x-2\right)\left(x-3\right)\left(x+2\right)\)
10 tháng 10 2021
\(a,=x\left(y^2-25\right)=x\left(y-5\right)\left(y+5\right)\\ b,=x\left(x-y\right)+2\left(x-y\right)=\left(x+2\right)\left(x-y\right)\\ c,=x^2\left(x-3\right)-4\left(x-3\right)=\left(x-2\right)\left(x+2\right)\left(x-3\right)\)
LT
27 tháng 12 2020
a) \(14x^2y-21xy^2+28x^2y^2\)
\(=7xy\left(2x-3y+4xy\right)\)
b) \(3x^2-5x-3xy+5y\)
\(=\left(3x^2-3xy\right)-\left(5x-5y\right)\)
\(=3x\left(x-y\right)-5\left(x-y\right)\)
\(=\left(x-y\right)\left(3x-5\right)\)
c) \(5a^3-20a\)
\(=5a\left(a^2-4\right)\)
\(=5a\left(a-2\right)\left(a+2\right)\)
d) \(2x+2y+x^2+2xy+y^2\)
\(=2\left(x+y\right)\left(x+y\right)^2\)
= \(=\left(x+y\right)\left(2+x+y\right)\)
19 tháng 10 2021
\(a,=6x\left(x-2\right)-7\left(x-2\right)=\left(6x-7\right)\left(x-2\right)\)
DP
1
23 tháng 12 2021
\(2a\left(x^2-9\right)=2a\left(x-3\right)\left(x+3\right)\)
HH
2
8 tháng 11 2021
a: \(=3\left(x-2y\right)\left(x+2y\right)\)
b: \(=5x\left(y^2-2yz+z^2\right)=5x\left(y-z\right)^2\)
AH
Akai Haruma
Giáo viên
7 tháng 9 2021
Lời giải:
a.
$3x^2+xy-4y^2=(3x^2-3xy)+(4xy-4y^2)=3x(x-y)+4y(x-y)=(x-y)(3x+4y)$
b.
$x^8-5x^4+4=(x^8-x^4)-(4x^4-4)$
$=x^4(x^4-1)-4(x^4-1)=(x^4-1)(x^4-4)$
$=(x^2-1)(x^2+1)(x^2-2)(x^2+2)$
$=(x-1)(x+1)(x^2+1)(x-\sqrt{2})(x+\sqrt{2})(x^2+2)$
c.
$x^3+3x^2+3x-7=(x^3+3x^2+3x+1)-8$
$=(x+1)^3-2^3=(x+1-2)[(x+1)^2+2(x+1)+4]$
$=(x-1)(x^2+4x+7)$
S
7 tháng 9 2021
a) \(3x^2+xy-4y^2=3x^2-3xy+4xy-4y^2\)
\(=3x(x-y)+4y(x-y)=(3x+4y)(x-y)\)
b)\(x^8-5x^4+4=x^8-x^4-4x^4+4\)
\(=x^2(x^4-1)-4(x^4-1)=(x^2-4)(x^4-1)\)
\(=(x-2)(x+2)(x^2-1)(x^2+1)=(x-2)(x+2)(x-1)(x+1)(x^2+1)\)
c)\(x^3+3x^2+3x-7=x^3+3x^2+3x+1-8\)
\(\left(x+1\right)^3-\sqrt{2}^3=\left(x+1-\sqrt[]{2}\right)\left(\left(x+1\right)^2+2\sqrt{2}x+2\right)\)
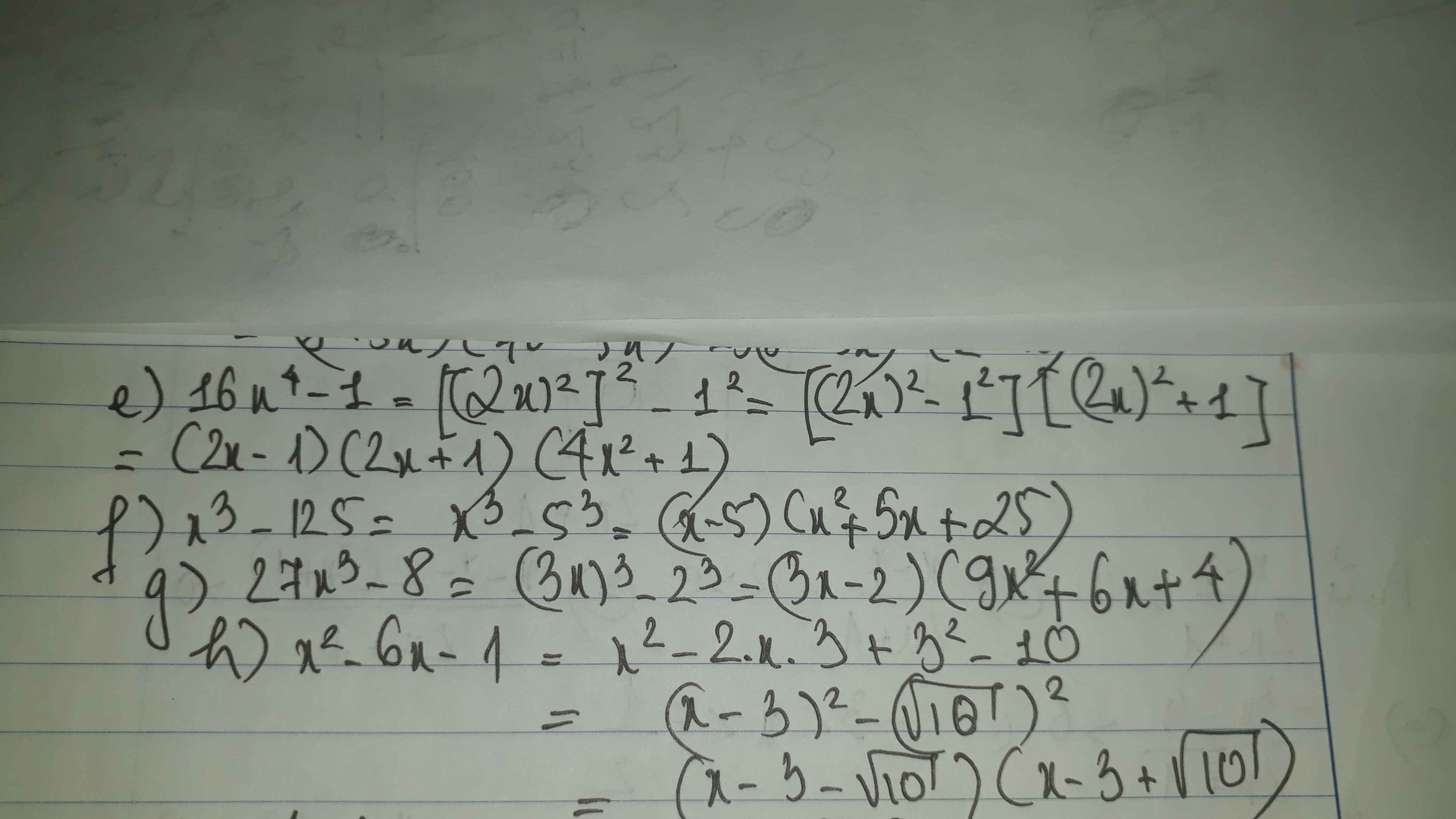
a) \(3x^2+2x-5=3x\left(x-1\right)+5\left(x-1\right)=\left(x-1\right)\left(3x+5\right)\)
b) \(25x^2-12x-13=25x\left(x-1\right)+13\left(x-1\right)=\left(x-1\right)\left(25x+13\right)\)
a) \(3x^2+2x-5\)
\(=2x^2+x^2+2x-5\)
\(=\left(\sqrt{2}x\right)^2-\left(-\left(x\right)^2-2x+\left(1\right)^2\right)-4\)
\(=\left(\sqrt{2}x\right)^2-\left(-x-1\right)^2\)
\(=\left(\sqrt{2}.x+x+1\right)\left(\sqrt{2}.x-x-1\right)\)