Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Theo công thức lãi kép suy ra:
T = A 1 + r 2 = 1. 1 + 0 , 5 % 24 = 1.127.160.000 đ ồ n g
Chọn C
Do lãi suất theo năm là 8% nên lãi suất tính theo tháng là
Cuối tháng 1, sau khi trả nợ 2 triệu, ông Bình còn nợ: 
triệu đồng.
Cuối tháng 2, sau khi trả nợ 2 triệu, ông Bình còn nợ:
triệu đồng.
Cuối tháng 3, sau khi trả nợ 2 triệu, ông Bình còn nợ 
….
Cuối tháng m, sau khi trả nợ 2 triệu, ông Bình còn nợ 0 đồng, nghĩa là
Ta có 
là tổng tất cả các số hạng của một cấp số nhân có
u
1
=
1
và công bội
q
=
n
+
1
gồm m số hạng 
Ta có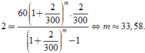 
Vậy ông Bình trả hết nợ sau 34 tháng.
Đáp án B
Bài toán tổng quát:
n: chu kỳ
A: khoản tiền cần vay
r: lãi suất/ chu kỳ
R: khoản tiền trả vào cuối mỗi chu kỳ
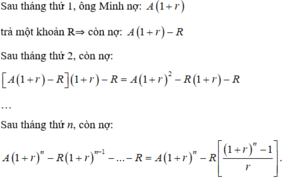
Đáp án B
Bài toán tổng quát:
n: chu kỳ
A: khoản tiền cần vay
r: lãi suất/chu kỳ
R: khoản tiền trả vào cuối mỗi kỳ
Sau tháng thứ 1, ông Minh nợ: A(1+r)
Trả một khoảng => còn nợ A(1+r) - R
Sau tháng thứ 2, còn nợ:
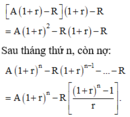
Sau n tháng, ông Minh trả hết nợ, tức là
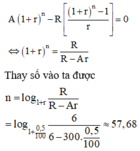
Tức là số tháng tối thiểu để ông Minh trả hết nợ là 58 tháng.
Đáp án A
Gọi a là số tháng gửi với lãi suất 0,5%/tháng, x là số tháng gửi với lãi suất 0,8%/tháng.
Khi đó tổng số tháng mà ông A gửi tiền vào ngân hàng là a + x + 3 tháng.
Suy ra số tiền ông A rút được cả vốn lẫn lãi là
10 000 000 × 1 , 005 a × 1 , 01 3 × 1 , 008 x = 10 937 826 , 469
⇔ 1 , 008 x = 10 937 826 , 469 10 000 000 × 1 , 005 a × 1 , 01 3 ⇔ x = log 1 , 008 10 937 826 , 469 10 000 000 × 1 , 005 a × 1 , 01 3
Chọn a = 1 → 6 ta thấy tại a = 4 thì x = 5. Vậy số tháng mà ông A phải gửi 4 + 3 +5 = 12 tháng.
Đáp án D
Số tiền phải trả hằng tháng bằng 96.1 % . 1 + 1 % 24 1 + 1 % 24 − 1 ≈ 4 , 52 triệu đồn
Đáp án D
Số tiền mà ông An nhận được là
T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 4 % 4 ≈ 59.895.767 đ ồ n g .
Đáp án D
Số tiền mà ông An nhận được là
T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 24 % 4 ≈ 59.895.767 đồng
