Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D.
Không mất tính tổng quát giả sử λ = 1.
Ta có:
Vì trên AB có 11 vị trí cực đại nên suy ra 5 < λ < 6.
(Dựa vào các đáp án suy ra chỉ có 5,3λ thỏa mãn).

Chọn đáp án D.
- Giả sử: MA = k. λ = 4k
Và MB = m. λ = 4m
+ Ta có: M A 2 + M B 2 ≤ A B 2
=> k 2 + m 2 ≤ 121 4
+ M ở xa A nhất khi và chỉ khi K m a x có thể a luôn có: MA ≤ AB = 22
=> 4K ≤ 22
=> K m a x = 5
- Điểm M cách xa A nhất một đoạn bằng: 5 λ = 20 cm thì ta cần có:
25 + m2 ≤ 121 4
=> m ≤ 2,2
=> m = 1 hoặc m = 2
- Với m = 1 ta có: MA - MB = 4 λ , tức là điểm M nằm trên cực đại số 4 cách A khoảng 20 cm và B là 4 cm
- Tương tự với m = 2 thì ta có:
+ Do mỗi đường cục đại này cho 2 điểm đối xứng nhau qua AB
=> Nên tổng là 4 điểm

Chọn D
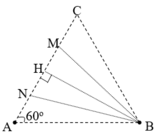
+ Xét N và M là hai điểm cực đại cùng pha liên tiếp trên AC
Điều kiện cực đại liên tiếp:
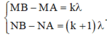
NB – MB + MA – NA = λ ⇔ NB – MB + MN = λ (1)
Điều kiện cùng pha liên tiếp:
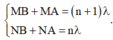
⇒ MB – NB + MA – NA = λ => MB – NB + MN = λ (2)
Cộng vế với vế của (1) và (2) ta được 2MN =2 λ =>NB=MB =>tam giác NBM cân; H là trung điểm của NM => BH ⊥ AH=>BH là đường cao trong tam giác đều ABC. Ta có:
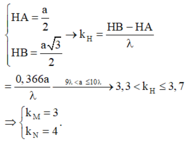
Xét điểm N:
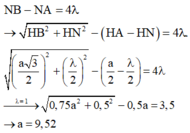
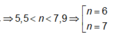
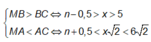
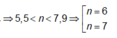
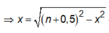
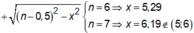
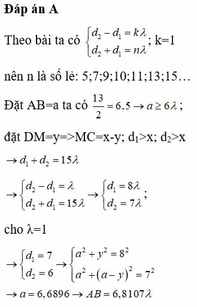







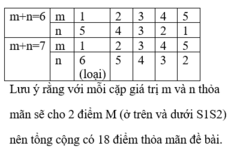
Đáp án B
Theo đề, trên AB có 9 vị trí mà ở đó các phần tử nước dao động với biên độ cực đại nên:
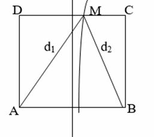
Vì I là trung điểm CD, ABCD là hình vuông nên
Vì hai nguồn A, B đồng pha nên giả sử:
Lúc đó, phương trình dao động tại điểm M là:
M là cực đại giao thoa bậc nhất:
Để M dao động ngược pha với các nguồn thì: