Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

12+1=13
Mình thì thích đọc các cuốn sách về lịch sử
Mấy cuốn sách mình đã đọc thì có Hoàng Lê nhất thống chí nói về những biến cố, sự kiện lịch sử từ thời chúa Trịnh Sâm đến hết thời Tây Sơn. Tác giả là Ngô Gia Văn Phái (Phái văn nhà họ Ngô)
Đại Việt sử kí toàn thư nói cụ thể về toàn bộ những sự kiện lịch sử từ thời Hồng Bàng đến năm 1675 thời vua Lê Gia Tôn nhà Lê. Tác giả là sử thần Ngô Sĩ Liên

Cách khác nè Phương: (đây là phương pháp chỉ ra một giá trị rồi chứng minh các giá trị còn lại không thỏa mãn)
a/ Giải
+) Với n = 0 thì \(n^2+2n+12=12\) không là số chính phương.
+) Với n = 1 thì \(n^2+2n+12=15\) không là số chính phương.
+) Với n = 2 thì \(n^2+2n+12=20\) không là số chính phương.
+) Với n = 3 thì \(n^2+2n+12=27\) không là số chính phương.
+) Với n = 4 thì \(n^2+2n+12=36=6^2\) là số chính phương.
+) Với n > 4 thì \(n^2+2n+12\) không là số chính phương vì:
\(\left(n+1\right)^2< n^2+\left(2n+12\right)< \left(n+2\right)^2\)
Thật vậy: \(\left(n+1\right)^2< n^2+2n+12\)
\(\Leftrightarrow n^2+2n+12-n^2-2n-1>0\)
\(\Leftrightarrow11>0\) (luôn đúng)
Do vậy \(\left(n+1\right)^2< n^2+2n+12\) (1)
C/m: \(n^2+\left(2n+12\right)< \left(n+2\right)^2\)
\(\Leftrightarrow n^2+4n+4-n^2-2n-12>0\)
\(\Leftrightarrow2n-8>0\) (luôn đúng do n > 4) (2)
Từ (1) và (2) suy ra với n > 4 thì \(\left(n+1\right)^2< n^2+\left(2n+12\right)< \left(n+2\right)^2\) hay \(n^2+2n+12\) không là số chính phương.
Vậy 1 giá trị n = 4
b/ +)Với n = 0 thì \(n\left(n+3\right)=0\) là số chính phương
+) Với n = 1 thì \(n\left(n+3\right)=4\) là số chính phương
+) Với n > 1 thì \(n\left(n+3\right)\) không là số chính phương vì:
\(\left(n+1\right)^2< n\left(n+3\right)< \left(n+2\right)^2\)
Thật vậy: \(\left(n+1\right)^2< n\left(n+3\right)\Leftrightarrow n^2+3n-n^2-2n-1>0\)
\(\Leftrightarrow n-1>0\) (đúng với mọi n > 1) (1)
Ta sẽ c/m: \(n\left(n+3\right)< \left(n+2\right)^2\)
\(\Leftrightarrow n^2+4n+4-n^2-3n>0\)
\(\Leftrightarrow n+4>0\) (luôn đúng với mọi n > 0) (2)
Từ (1) và (2) suy ra với mọi n > 1 thì \(n\left(n+3\right)\) không là số chính phương.
Vậy n = 0;n = 1

Gọi số sách trên 2 giá lúc đầu lần lượt là x và y cuốn (với x>100, y>0)
Do hai giá có tất cả 1820 cuốn sách nên: \(x+y=1820\)
Sau khi chuyển từ giá thứ nhất sang giá thứ hai 100 cuốn (đồng nghĩa giá thứ nhất giảm 100 cuốn và giá thứ hai tăng 100 cuốn) thì số sách 2 giá bằng nhau nên:
\(x-100=y+100\Rightarrow x-y=200\)
Ta được hệ:
\(\left\{{}\begin{matrix}x+y=1820\\x-y=200\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1010\\y=810\end{matrix}\right.\)

gọi số sách lúc đầu ở giá 1 là x (cuốn)
ở giá 2 là y (cuốn)
Ta có phương trình tổng số sách ở 2 giá là x+ y = 450 (1)
theo đề bài ta có phương trình thứ hai là y + 50 = 4/5 (x-50) => 5(y+50) = 4(x-50) => 4x -5y = 450 (2)
giải hpt (1)(2) => x = 150; y = 300
Vậy số sách lúc đầu ở giá 1 là 150 ; giá 2 là 300 cuốn

?????????????????????????????????????????????????????????????????????????????????????????

Gọi số sách ở giá thứ nhất là x ( cuốn)
Số sách ở giá thứ hai là y (cuốn), (x, y∈ N*; x> 50, x< 450, y< 450)
Hai giá sách có tất cả 450 cuốn nên x+ y = 450 (1)
Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x- 50 và số sách ở giá thứ hai là y+ 50
Theo đầu bài ta có:
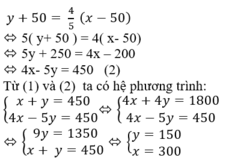
Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.
Bạn đọc THE CALL OF THE WILD đi, hay lắm!!
ukm cảm ơn bn nha!